函数的导数(一阶)等于1


选自《运动论》第16页
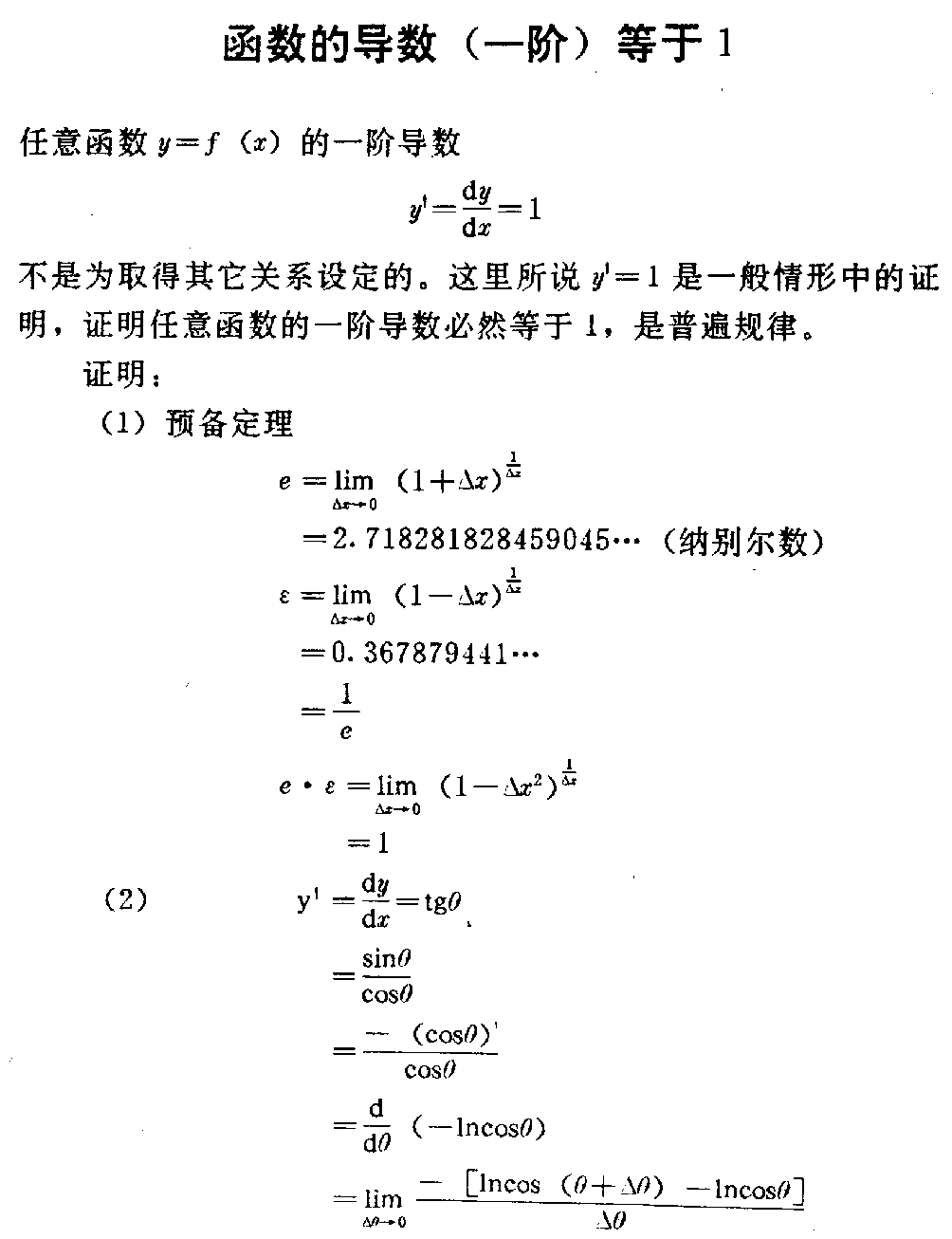
下载函数的导数(一阶)等于1 任意函数y=f(x)的一阶导数 y=dydx=1 不是为取得其它关系设定的。这里所说y=1是一般情形中的证明,证明任 意函数的一阶导数必然等于1,是普遍规律。 证明: (1)预备定理 e=limΔx→0 (1+Δx)1Δx =2718281828459045…(纳别尔数) ε =limΔx→0(1 -Δx)1Δx =0367879441… =1e e·ε= limΔx→0(1-Δx2)1Δx =1 (2)y=dydx=tgθ =sinθcosθ =-(cosθ)cosθ =ddθ(-lncosθ) =limΔθ→0-[lncos (θ+Δθ)-lncosθ]Δθ =limΔθ→0(1Δ θ)ln[cosθcosθ(θ +Δθ)] =lnlimΔθ→0[ cosθcosθ·cosΔθ-sinθ·sin Δθ]1Δθ 其中 limΔθ→0cosΔθ=1 limΔθ→0sinΔθ= Δθ(一阶无穷小) limΔθ→0tgθ·sin Δθ=Δθ(仍为一阶无穷小) 则y=lnlimΔθ→0 (11-Δθ)1Δ θ 这里11-Δθ=1+Δ θ1-Δθ2 因limΔθ→0(1-Δθ 2)1Δθ=1 则y=lnlimΔθ→ 0(1+Δθ)1Δθ =lne =1 当然,如果y是复合函数,则有二阶以上高阶导数,高阶导数并不等于1。 因此, 复合函数为y时,有 y=y(lny)— — (y/y) 一般函数为y时,有 1=y(lny)——(1 /y) 使用(y/y)、(1/y)两式可轻易求得原函数。 例,已知y=nxn-1,求y 令y=1 nxn-1=1 nxn·1x =1 根据(1/y)式 nxn(lnx)=1 xn(lnxn)=1 仍根据(1/y)式,得 y=xn 例,已知y=uv+vu,求y 令y=1 1=uv+vu 根据(y/y)式 1=u[v(lnv)]+v[u( ln u)] =uv[(lnv)+(lnu)] =uv[lnv+lnu] =uv(lnuv) 根据(1/y)式 y=uv 这是使用(1/y)、(y/y)两式求取原函数的一种新尝试。是“原函 数统一公式”的另一形式。参考本书“数学的关联”一节。 这两个式子的作用又是双向的,可求原函数,同时又可求导数。
