数学的关联

选自《运动论》第313页
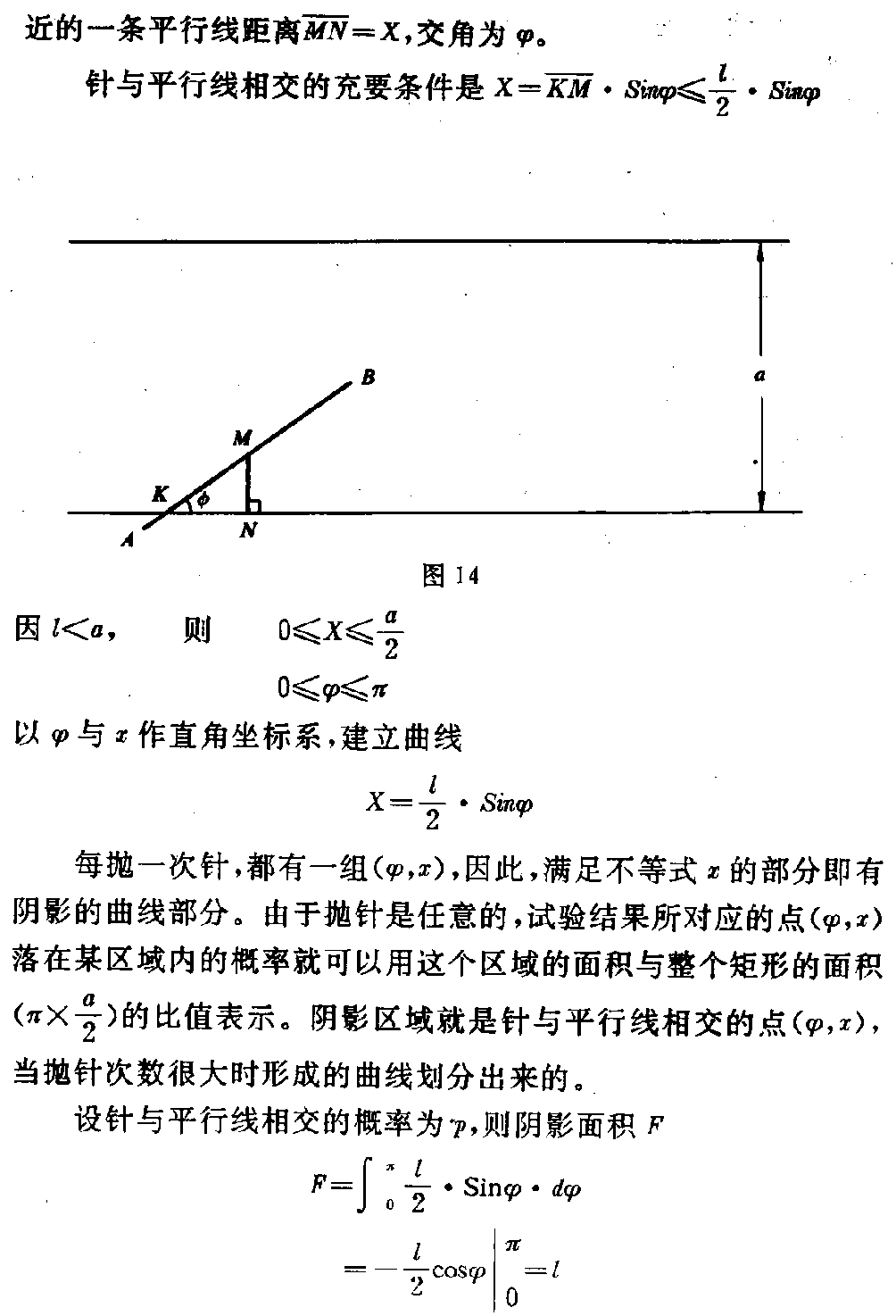
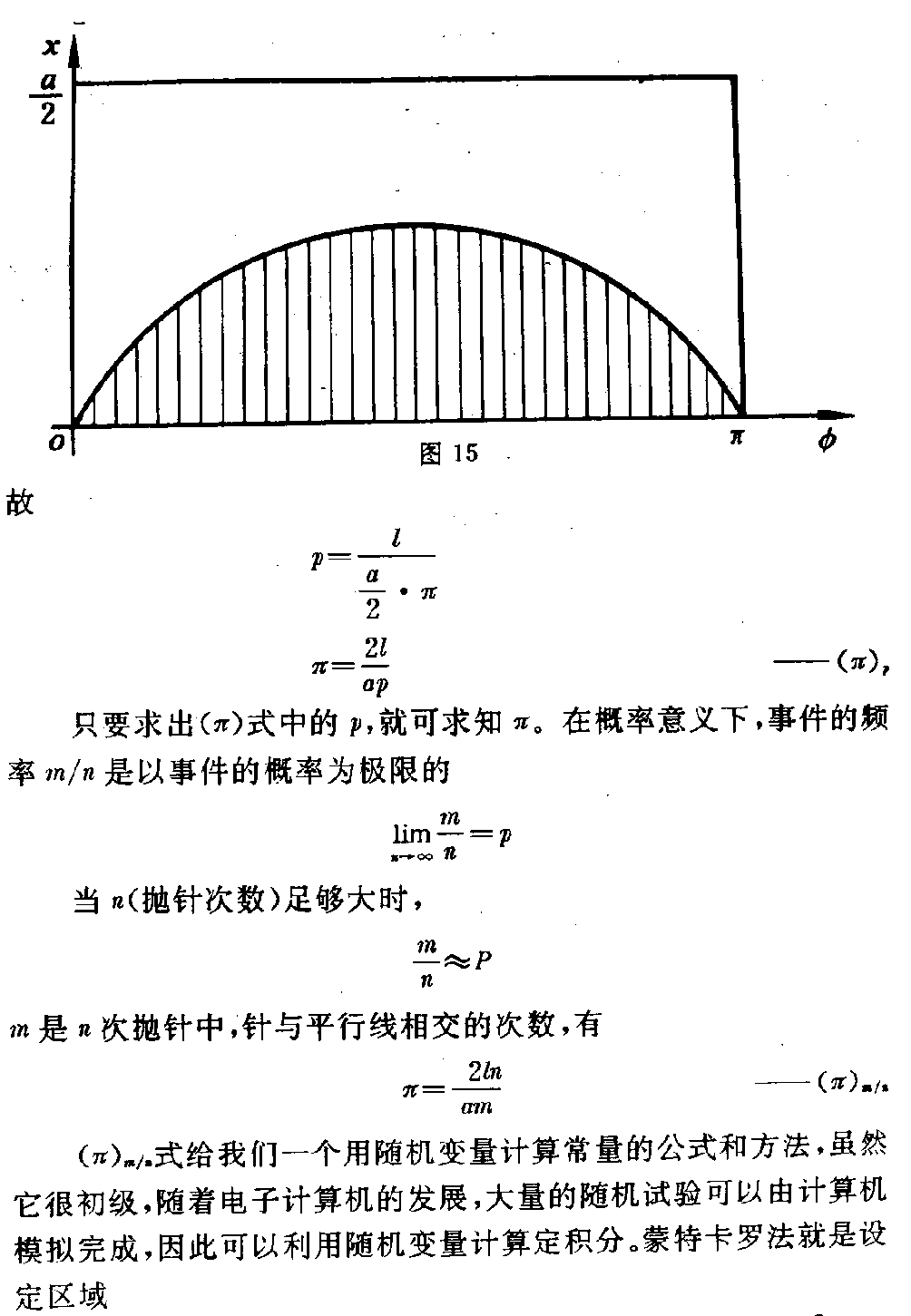
下载
数学的关联
世界是单纯或然的，因而具有必然偶然性呢？还是单纯必然的
，因而具有必然因果性呢？是平衡的还是非平衡的？是守恒的还是非守恒的？
至今各家都必须通过自己的数学形式逻辑来表达，来证明，并以其数学形式逻
辑为根源的中心，归纳或演绎自家对物质世界，或认定物质世界的运动形式，
或提高到哲学观念。
不论数学及其逻辑形式怎样分支，差异渐著，我们总知道数学存在统一根源外
，各分支间还存在着“数学的关联”，或者说，它们间存在相互的变换规律
，这种规律有的已被发现，有的尚待探求。假如人们逐一发现这些变换，从数
学的逻辑根源谈起，大家观点的逼近是有可能的。因此，与其讨论物理世界，
纵谈哲学观念，不如数学的逻辑演绎及其关联的探索来得干脆、有力、了然。
本文要谈及
（１）单纯或然世界与因果必然世界两种观念的数学逻辑根源及其关联。
（２）数学的代数关联。
现谈出一点个人的浅见。
（一）圆周率π与概率的关联
蒲丰（Ｂｕｆｆｏｎ）的抛针求π法。
先在纸上划一簇等距离的平行线，然后取一根普通的缝衣针在这簇平行线上任
意丢掷，统计ｎ次抛针中与平行线相交的次数ｍ。
设相邻平行线间的距离为ａ，针长ｌ（ｌ＜ａ），ｌ
＝ＡＢ，基中点Ｍ到最近的一条平行线
距离ＭＮ＝Ｘ，交角为φ。
针与平行线相交的充要条件是Ｘ＝ＫＭ·Ｓｉｎφ≤ｌ２·Ｓｉｎφ
图１４

因ｌ＜ａ，则０≤Ｘ≤ａ２
０≤φ≤π
以φ与ｘ作直角坐标系，建立曲线
Ｘ＝ｌ２·Ｓｉｎφ
图１５
每抛一次针，都有一组（φ，ｘ）
，因此，满足不等式ｘ的部分即有阴影的曲线部分。由于抛针是任意的，试验结果
所对应的点（φ，ｘ）落在某区域内的概率就可以用这个区域的面积与整个矩
形的面积（π×ａ２）的比值表示。阴影区域就是针
与平行线相交的点（φ，ｘ），当抛针次数很大时形成的曲线划分出来的。
设针与平行线相交的概率为ｐ，则阴影面积Ｆ
Ｆ＝
π０ｌ２·Ｓ
ｉｎφ·ｄφ
＝－ｌ２ｃｏｓφπ
０＝ｌ故
ｐ＝ｌａ２·π
π＝２ｌａｐ——（π）ｐ
只要求出（π）式中的ｐ，就可求知π。在概率意义下，事件的频率ｍ／ｎ是
以事件的概率为极限的
ｌｉｍｎ→∞ｍｎ＝ｐ
当ｎ（抛针次数）足够大时，
ｍｎ≈Ｐ
ｍ是ｎ次抛针中，针与平行线相交的次数，有
π＝２ｌｎ
ａｍ——（π）ｍ／ｎ
（π）ｍ／ｎ式给我们一个用随机变量计算常量的公式和方法，虽然它
很初级，随着电子计算机的发展，大量的随机试验可以由计算机模拟完成，因
此可以利用随机变量计算定积分。蒙特卡罗法就是设定区域
０≤ｆ（ｘ）≤１
０≤ｘ≤１求Ｉ＝１０ｆ（ｘ）
ｄｘ的方法。由几何概率知，随机变量点Ｍ在曲线
ｙ＝ｆ（ｘ）
下方的区域概率ｐ刚好是该区域面积〔全区域（１×１）的面积等于１〕即
Ｐ＝１０ｆ（ｘ）ｄｘ
因Ｐ≈ｍｎ
则ｍｎ＝１０ｆ（ｘ
）ｄｘ
检验随机点（ξｉ，ηｉ）＝１，２，３…ｎ是否使不等式
ηｉ≤ｆ（ξｉ）
成立，则可知
ｙ＝ｆ（ｘ）
区域内的点ｍ，　ｍ／ｎ即积分
１０ｆ（ｘ）ｄｘ
的近似值。这项工作交计算机很快就可完成。
我们注意到一个简单的事实：
“定积分在特定限内等于一个相对数的极限值。即限定域为０≤ｘ≤１，０≤
ｆ（ｘ）≤１的定积分等于某项概率”。
既然计算机能够替代人的行为去模拟试验给定积分表达一个相对数，那么就有
可能在更为广泛的逻辑形式中也存在这种关系，重要的价值不在于求π，而在
于“与圆周率相关的相对数ｍ／ｎ的多种形式与或然率建立的对等关系”，
即或然偶然逻辑与因果必然逻辑的关联。
下一节将进一步把概率的一般函数表达成这种“相对数”（三角函数）来显示
两种逻辑（或然偶然逻辑与因果必然逻辑）的关联，数学关系之间的变换。
（二）  或然率函数与三角函数（相对数）的关联
一般或然率函数可以下式表示
ｙ＝ｅｘ２
用对数求导法，将上式对ｘ取导
ｙ＝ｙ（ｌｎｅ－ｘ２）
＝ｙ（－ｘ２）
＝ｙ（－２ｘ）
该微分方程的解是ｙ＝ｃｏｓθ
ｙ＝ｓｉｎθ
（１）当ｙ＝ｃｏｓθ时
－（ｃｏｓθ）ｃｏｓθ＝２ｘ
－－ｓｉｎθｃｏｓθ＝２ｘ
ｔｇθ＝２ｘ
（２）当ｙ＝ｓｉｎθ时－
（ｓｉｎθ）ｓｉｎθ＝２ｘ
－ｃｏｓθｓｉｎθ＝２ｘ
－ｃｔｇθ＝２ｘ
有解
ｃｏｓθ＝ｅ－ｘ２
ｓｉｎθ＝ｅ－ｘ２
表现了或然率函数与相对数（三角函数）的关联。
现用积分法再求，以示校验。将原或然率函数开平方
ｙ１２＝ｅ－ｘ２
２
取自然对数
１２ｌｎｙ＝－ｘ２２
用积分公式
ｌｎｙ＝∫ｄｙｙ＋ｃ
ｘｎ＋１ｎ＋１＝∫Ｘｎｄｘ＋ｃ
有１２ｙ０ｄｙｙ＝－Ｘ０ｘｄ
ｘ
－ｄｙｙ＝２ｘｄｘ
－ｙｙ＝２ｘ
显然ｙ的解仍是ｃｏｓθ、ｓｉｎθ。
我们说圆函数的三角函数之所以是“因果必然”的，在于它们有恒等关系
１＝ｃｏｓ２θ＋ｓｉｎ２θ
从物理学角度说，这种关系即一种守恒关系，因此它是“封闭式”的关系，即
产生ｃｏｓθ值是因为ｓｉｎθ值的减少，或相反，但它们各自平方
的总和不变，恒等，正所谓“有因必有果”的可预见性质。
但或然率函数ｅ－Ｘ２是开放型的，ｅ是个无理又无理的数（纳别尔
数），ｘ存在于－∞≤ｘ≤＋∞区间，在还不曾知道这种“关联”之前，公
式所描述的物理现象总是某种“必然偶然”的，只有同样的物理行为终止并达
到相当数次之后才能接近知道结果的范围，所以又是不可预见的。
随着人们实践经验的增加，科学哲学思想的逐步健全，尤其辩证逻辑被人们广
泛接受与广泛应用于实践活动，才发觉任何事物中构成矛盾对立双方的统一，
同一运动事物都具有双重性质。
数学尤其如此，因为概括说，数学可以是自然、社会、思维等等宇宙存在的对
称，任何一个大学科内都有质的与量的运动规律，只不过人们知道这种规律存
在于该学科的形式是怎样的，它的数学语言又是怎样的实在不多不够罢了。我
们所处的人类社会发展时代是刚刚为人们认识数学功能广阔存在的时代，认识
刚刚起步的时代，随着社会的发展，人类社会各领域里“识数”的人将越来越
多。
具体地说，数学内部“对称”现象的出现早已为人们认识、接受。“＋”与“
－”，“×”与“÷”，微分与积分等等比比皆是。
当我们知道圆函数时，那是在笛卡尔坐标诞生之后，其实勾股定理早已出现。
随着微积分的完善、指数、对数的发展，人们又观察到虚数，从而发展了复数
以及与圆函数对称的双曲函数，才算完全了一种对称，中间过程何其长久，对
于人而言，要发现需时间间隔，而对数学而言，“对称”早就存在那里了。只
有后人把这个时间间隔有可能当成瞬间，排除“人的介
入”认识规律并系统接受，而且发觉了圆与双曲两函数间的关联和变换。
但是，用数学语言说明自然现象，解释和归纳社会将又是另一回事，同样也要
人们的认识过程，要人们的实践和经验以及验证。总之还要时间，尽管数学公
式已经摆在那里。如：
ｃｏｓθ＝ｅ－Ｘ２
已经严密逻辑过程建立在这里，数学家可以数学眼光一目了然，然而要物理学
家承认量子运动规律的偶然性与天体运动规律的必然性是“对立统一”的，恐
怕一时还解决不了。因为除了每个人都具有成长过程形成的“固有惯性”需被
克服之外，还要时间来取得大量的实践验证。
为此，笔者还是愿意从多方面的数学关联，从理论的预见性上加以阐述。下节
从另一角度谈这一关联。
（三）  圆周率π、三角函数与或然率的多途径关联
计算圆周率π的方法也间接反应出这种关联。近代的反正切函数的级数式求π
，可获收敛迅速的效果。大家知道，公比为ｑ的几何级数
１＋ｑ＋ｑ２＋ｑ３＋…＋ｑｎ－１＋…
若｜ｑ｜＜１该级数收敛，有和式
１１ｑ＝１＋ｑ＋ｑ２＋ｑ３＋…＋
ｑｎ－１＋…
令 ｑ＝－ｘ２，｜ｘ｜＜１，则
１１＋Ｘ２＝１－Ｘ２＋Ｘ４－Ｘ
６＋…＋（－１）ｎ－１Ｘ２ｎ－２＋…
用积分公式
Ｘ０ｄｘ１＋Ｘ２＝Ａｒｃｔｇｘ
Ｘ０Ｘｎｄｘ＝Ｘｎ
＋１ｎ＋１
对上级数在其收敛区间－１＜ｘ＜１积分，得：
Ａｒｃｔｇ
ｘ＝ｘ－Ｘ３３＋Ｘ５５－…＋（－１）ｎ－１Ｘ２ｎ－１２ｎ－
１＋…
｜Ｘ｜越近于０，该级数的收敛速度越快。已经获得的求π公式，如马丁公式
π４＝４Ａｒｃｔｇ１
５－Ａｒｃｔｇ１２３９
我们注意到公式
ｖ０
ｄｖ１＋ｖ２＝Ａｒｃｔｇｖ
若令θ＝Ａｒｃｔｇｖｖ＝２ｘ
则
２ｘ＝ｔｇθ
＝ｓｉｎθｃｏｓθ
＝－（ｃｏｓθ）ｃｏｓθ
＝－ｄｄθｌｎ　ｃｏｓθ
各以ｄｘ、ｄθ为积分变量取定积分
ｘ０２ｘｄｘ＝－θ０（ｌｎ  ｃｏｓθ）′ｄθ
ｘ２＝ｌｎ  ｃｏｓθ
从而得到ｅｘ２＝ｃｏｓθ
即ｅ∫ｙ’ｄｘ＝ｃｏｓθ
与“二、或然率函数与三角函数之关联”一节所获关系全同。由多方面证明所
得或然率函数与三角函数之关联已不是偶然。
如果
ｃｏｓθ＝ｅｘ２
则有ｓｉｎθ＝１ｅ２ｘ２
ｔｇθ＝ｅ２ｘ２１
ｃｔｇθ１ｅ２ｘ２－
１
ｓｅｃθ＝ｅｘ２
ｃｓｃθ＝１１ｅ－２ｘ
２
（四）物理实在与“数学关联”的关联
受因斯坦相对论的数学基础是由守恒原理展开的，即光速恒定原理：
ｒ＝ＣΔｔ
其中，Ｃ为光的速度，Δｔ为时间差，ｒ是光在Δｔ时间内运行的距
离，即线性空间。
双方平方并以坐标差Δｘγ表示ｒ，有
∑（３）（Δｘγ）２Ｃ２
Δｔ２＝０
他将线空间在坐标中分解为三维，时间看成第四维，可表示为：
∑（４）Δｘγ２＝
Δｘ１２＋Δｘ２２＋Δｘ３２＋Δｘ４２＝０
其中
ｘ４＝ｉ　ｌ＝ｉ　Ｃ　ｔｉ＝１
显见，上式就是：“四维商高定理的守恒式”，然后他将它经特殊洛伦兹坐标变
换，得：
ｘ１′＝ｘ１ｃｏｓφ－ｘ２ｓｉｎφ
ｘ２′＝ｘ１ｓｉｎφ＋ｘ２ｃｏｓφ
ｘ３′＝ｘ３
ｘ４′＝ｘ４
ｘ１′＝ｘ１ｃｏｓφｘ４ｓｉｎφ
ｘ４′＝ｘ１ｓｉｎφ＋ｘ４ｃｏｓφ
ｘ２′＝ｘ２
ｘ３′＝ｘ３
两组新旧坐标值关系，其中，
ｘ１′＝ｘ１ｃｏｓφ－ｉ　ｌｓｉｎφ
ｌ′＝－ｉ　ｘ１ｓｉｎφ＋ｌ　ｃｏｓφ
当ｘ１′＝０，有ｘ１＝ｖ　ｌ，因此，
ｖ＝ｉｔｇφ
ｓｉｎφ＝－ｉ　ｖ１－ｖ２

ｃｏｓφ＝１１ｖ２

ｘ１′＝ｘ１－ｖ　ｌ１－ｖ
２
ｌ′＝ｌ－ｖｘ１１－ｖ２
参看，爱因斯坦，相对论的意义，科学出版社，１
９７９年。
这种三维空间加一维时间的四维旋转变换仍离不开三角函
数守恒关系
１＝ｃｏｓ２φ＋ｓｉｎ２φ
我们看到他重点是获取ｘ１与ｘ４的变换，实际是空间与时间的守恒关系
，空间减少是因为时间延长，或相反。
抛开上述爱因斯坦的数学推导，现在假如有
ｙｘ＝１
将ｙ也类似当成三维，ｘ为一维虚值，也会建立
∑（３）Δｙ２Δｘ２＝０
（以坐标差表示）
最后仍可得到ｙ／ｘ＝１的恒等式
１＝ｃｏｓ２θ＋ｓｉｎ２θ
然而爱因斯坦所得结果充填了物理内容，后者的ｙ／ｘ＝１未加入物理内容，纯是
数学关系。之所以同时例举对比，用意在于它们的逻辑是同一的，不论它们各
自解释的对象有多么大的差别，都无关紧要。
那么，如果或然率函数的一般式是
ｙ＝ｅ－ｘ２
是量子力学所赖以描述的数学模型，相关于微观物质世界运动，我们就找到了
“单纯或然世界”与“因果必然世界”数学的逻辑的相关道路：
（１）由数学关联导出物理实在。
在“各相对数的或然性关系”一节已知
ｃｏｓθ＝ｅ－ｘ２ｔｇθ＝ｅ２
ｘ２－１
若爱因斯坦给出
ｃｏｓθ＝１１ｖ２
则１ｖ２＝ｅｘ２
ｖ＝１ｅ２ｘ２
＝ｉｅ２ｘ２１
故ｖ＝ｉｔｇθ
此式恰恰是爱因斯坦获得的公式之一。
（２）由物理实在导出数学关联
相对论给出
ｓｉｎθ＝－ｉ　ｖ１－ｖ
２
又因ｖ＝ｉｅ２ｘ２１
ｅｘ２＝１－ｖ２
ｓｉｎθ＝１ｅ－２ｘ２
ｃｏｓθ＝ｅ－ｘ２
反推亦然。
因此，可知狭义相对论各式与或然率函数描绘的量子力学粒子运动有相互对应
的物理学意义。在狭义相对论看来是虚值的物理世界恰恰是或然率函数描绘量
子力学的实值物理世界。由于“参考系”不同，各自描述的物质运动互为虚实
，所争所论的实质是同一规律的两个对称面。也可认为，宇宙运动规律（为相
对论阐述）与粒子运动规律（为量子力学阐述）雷同。
此时，我这样说，仅就数理推断的某个别关系而言，因此排除实验与观测对此
结论的验证。
（五）数学的代数关联
大家知道，导数定义给出了求导数的一个构造性算法，而
不定积分的定义却没有这个特点，且初等函数的导数仍是初等函数，不少初等
函数的不定积分却不是初等函数，或者说就现有的不定积分定义和积分法则解
决不了某些初等函数的不定积分。
但是蒙特卡逻给了我们一个求定积分的“普遍适用法”、“统一法”，它不必依
赖积分公式，对任意形式函数的定积分，只要取范围
０≤ｘ≤１
０≤ｆ（ｘ）≤１
定积分
１０ｆ（ｘ）ｄｘ
都等于概率频率ｍ／ｎ的极限：
ｌｉｍｎ→∞ｍｎ＝１０ｆ（ｘ）ｄｘ
现在已经知道，它对解线性方程组、微分方程已有专门的电子计算机用程序，
很快可获解。
这项“统一”法的意义在于概率值表达的数能够与定积分建立直接关系。笔  
者发现，蒙特卡罗理论的建立与蒲丰求圆周率π直接相关，或者说，蒙特卡罗
法所求的数（定积分）与弧度数直接相关，所以它与相对数相关。
既然计算机能够代替人的行动，使随机量（实验次数）趋近绝对无穷大，那么
就一定可以通过相对数找到相
对无穷大取代绝对无穷大，即找到两种无穷大间的变换，达到依靠仅有的计算
关系而不是依靠计算机来实现我们要求的数（积分）。
事实上，这就是存在一个与微分的构造性定义算法相类似的表达积分的定义，
任意函数的积分都可以该定义的算法求得。弧度数与绝对数的变换关系就是这
种关系：
设一个待求的定积分
ｙ＝ｘ０φ（ｘ）ｄｘ
ｙ＝ｄｙｄｘ＝φ（ｘ）
为已知函数
因为曲线ｙ上处处的切线与水平轴夹角τ的正切值等于导数值
ｄｙｄｘ＝ｔｇτ
故τ＝Ａｒｃ　ｔｇ（ｄｙ
ｄｘ）
＝Ａｒｃ　ｔｇφ（ｘ）
＝φ（ｘ）０ｄφ（ｘ）１＋φ（ｘ
）２（公式）
则
ｄτｄφ（ｘ）
＝１１＋φ（ｘ）２
设函数φ（ｘ）连续，可导，令
ｄφ（ｘ）ｄｘ＝ｙ″
有
ｄτｄφ（ｘ）ｄφ（ｘ）ｄｘ＝ｙ″１＋φ
（ｘ）２
＝ｄτｄｘ
另一方面
ｙ＝ｄｙｄｘ＝
ｔｇτ
＝ｓｉｎτｃｏｓτ＝－
（ｃｏｓτ）ｃｏｓτ
＝ｄｄτ（－
ｌｎ  ｃｏｓτ）
则

τｏｔｇτｄτ＝－ｌｎ  ｃｏｓ
τ

ｙ＝〔－ｌｎ  ｃｏｓτ〕·ｄｘｄτ
最后得到
ｙ＝（１＋ｙ２ｙ″）ｌｎ〔
ｓｅｃ｛Ａｒｃ  ｔｇ（ｘ）｝〕
——（ｙ）
也可写成
ｓｅｃτ＝ｅｙＭ
ｃｏｓτ＝ｅ－ｙＭ
（ｙ）式就是原函数的“构造性定义”，通过运算过程可知，它就是“数弧变
换”，是一种自然对数。
现在对它求导、校验，观察是否正确。
公式
（ｌｎｆ）＝ｆｆｄ
ｖｎ＝ｎｖｎ－１ｄｖ
ｄ  ｓｅｃτ＝ｓｉｎτｃｏｓ２τｄτ
令Ｍ＝１＋ｙ２ｙ″
则
ｙ＝ｄｄｘ
〔ｓｅｃ｛Ａｒｅ  ｔｇ（ｙ）｝〕Ｍ〔ｓｅｃ｛Ａ
ｒｃ  ｔｇ（ｙ）｝〕Ｍ
＝Ｍ·ｄｄｘ〔
ｓｅｃ｛Ａｒｃ  ｔｇ（ｙ）｝〕ｓｅｃ｛Ａｒｃ  ｔ
ｇ（ｙ）｝
＝Ｍ·ｔｇτ·ｄτｄｘ
因为Ｍ＝ｄｘｄτ
得ｙ＝ｔｇτ
验证正确。
ｙ是任意函数，则ｙ也是任
意函数ｙ的原函数。导数ｙ与原函数ｙ的这项关联称为“数学的代数关联”。
我们看到这项关联的存在有个奇怪现象：
（１）从导数ｙ到原函数ｙ
产生
ｙ＝Ｍｌｎ  ｓｅｃτ的
原因ｙｔｇτ——（结果）（１）——（原因）（１）
（２）从原函数ｙ到导函数ｙ
只有ｙ＝ｔｇ
τ，
才有ｄｙｄｘ
＝ｄｄｘ〔Ｍｌｎ  ｓｅｃτ〕＝ｔｇ
τ——（原因）（２）
——（结果）（２）
这是因为
ｙ＝ｔｇτ时，才有
Ｍ＝１＋ｙ２ｙ″＝ｓｅ
ｃ２τｓｅｃ２τ＝１
才有
ｄｄｘｙ＝ｄｄｘ〔Ｍｌｎ  ｓｅｃτ〕＝ｄ
ｄｘｌｎ  ｓｅｃτ＝ｔｇτ
如果要ｙ＝ｔｇτ（原因）（２），何必去求（结果）（２）？（
原因）（２）成为（结果）（２）这种现象正是一种悖论，我们称之为“
积分悖论”。
式（原因）（２）与式（结果）（２）是同一个，写成
（结果）（２）＝（原因）（２）现象。
或者说，产生（结果）（１）与产生（结果）（２）的原因
都是（原因）（１）＝（原因）（２）
●这个悖论的根源在于，如果Ｍ＝１即
Ｍ＝ｄｘｄτ＝１
得出ｄｘ＝ｄτ
的结论
在单位圆中ｄτ＝ｄＳ（τ＝Ｓ），有
ｄｓ＝ｄｘ２＋ｄｙ２
ｄｘｄｓ＝ｃｏｓτｄｙｄｓ＝ｓｉｎτ
如果ｄτ≠ｄｓ，则引出
ｄτｄｓ＝Ｋ
正是曲线的曲率。一般情形Ｋ≠１，因此必有Ｋ介入原函数，这里的
ｄｘｄτ＝Ｍ
应理解为“曲线上任意点对于横轴之偏曲率的倒数”。偏曲率类似偏导数。Ｋ
≠１则Ｍ≠１。
●我们注意到
ＭＫ＝ｄｘｄτ·
ｄτｄｓ
＝ｄｘｄｓ
＝ｃｏｓτ
＝１（１＋ｙ２）１／２
＝ｅ－ｙＭ
＝ｅ－１Ｍ∫ｙｄｘ
其中ｅ－∫ｙｄｘ是一阶线性微分方程的基本解。
ｅ－１Ｍ
∫ｙｄｘ有可能是更大范围微分方程的解，这里就不单作
数学分析了，有待更多智者的介入，笔者能力有限。
●以“偏曲率”角度出发，曲率Ｋ的相关，使因Ｋ≠１，则必使Ｍ≠１，观
察ＭＭ＝１＋ｙ２ｙ″
要求ｙ″≠０，也即要求ｙ＝φ（ｘ）可导。
（ｙ）式的求得表明，积分问题可以是函数Ｇ
ｙ＝Ｇ〔φ（ｘ）、φ（ｘ）、φ″（ｘ）〕
的代数运算（ｙ）式来代替吗？
●此外，若考虑积分常量，可以将此常量看成原函数ｙ的一部分。
ｙ＝Ｍｌｎ  ｓｅｃτ＋Ｍｃ
●（ｙ）式的数弧分析
令＝ｌｎ  ｓｅｃτ，
ｙ⌒
＝Ｍｌｎ  ｓｅｃτ＝Ｍ
因为数的根源是ｙ＝ｔｇτ视为直角三角形。
ｙ⌒
被视为弧，因为它等于Ｍ。有
ｙ⌒
ｄτ＝ｄｘ
出现两积分元素对等，此种状态与本文“三、圆周率π、三角函数与或然率的
多途径关联”最后求２ｘ的积分使用方法全同。但此时已经将原函数
ｙ⌒
与作为积分要素参加积分里来，又升了格。于是
τｏｙ⌒
ｄτ＝
ｘｏｄｘ
ｙ⌒
与在这里又成为积分对象。若令
Ｙ⌒
＝∫ｙ⌒ｄτ＋ｃ
则ｄＹ⌒
ｄτ＝ｙ⌒
ｙ⌒又是
Ｙ⌒的导数
Ｙ′⌒。同样有
＝∫ｄｘ＋ｃ
则ｄｄｘ＝

又是的导数。故
ｄ
Ｙ⌒ｄτ
＝Ｍｄ
Ｙ⌒ｄｘ
Ｙ′⌒＝Ｍ
′
可见，、、
ｙ⌒、
Ｙ⌒、都可以
是各阶段上的导数，同时也
是各阶段上的原函数。导数与原函数只是相对的称谓，它们应当总是“中介状
态”的（ｙ可导）。
（六）导函数与原函数的相对性质
（导数概念的外延与原函数概念的引伸）
ｄｙｄｘ＝
ｔｇθ
＝ｓｉｎθｃｏｓθ＝－
（ｃｏｓθ）
ｃｏｓθ＝ｄｄθ（
－ｌｎ  ｃｏｓθ）
＝ｌｉｍΔθ→０－〔
ｌｎ  ｃｏｓ（θ＋Δθ）
－ｌｎ  ｃｏｓθ〕Δθ
＝ｌｉｍΔθ→０１Δ
θ·ｌｎｃｏｓθｃｏｓ
（θ＋Δθ）
＝ｌｎｌｉｍΔθ→０
ｃｏｓθｃｏｓθ·ｃｏｓΔθ－ｓｉｎθ·ｓ
ｉｎΔθ１Δθ
其中
ｌｉｍΔθ→０ｃｏｓ
Δθ＝１
ｌｉｍΔθ→０ｓｉｎΔθ＝Δ
θ（一阶无穷小）
ｌｉｍΔθ→０ｔｇθ·ｓｉｍ
Δθ＝Δθ（仍为一阶无穷小）则

ｄｙｄｘ＝ｌｎ
ｌｉｍΔθ→０（１１－Δθ
）１Δθ
＝ｌｎｌｉｍΔθ→０（
１＋Δθ１－Δθ２）１Δθ

因为这里
ｌｉｍΔθ→０（１－Δ
θ２）１Δθ＝１（参看“两个
新重要极限”）
于是
ｄｙｄｘ＝ｌｎｌｉ
ｍΔθ→０（１＋Δθ）
１Δθ
＝ｌｎ　ｅ
＝１
任意函数ｙ＝ｆ（ｘ）的导数都等于１。
这是一个相对于原函数存在的一般概念，它的意义为，就原函数与导数的相对性
而言，函数ｙ的导数ｙ可以看成为函数ｙ的“１”，ｙ可以看成为ｙ的相
对无穷大，并且共同存在于自然对数关系中。它的来源过程已经指明。
从代数角度看
ｄｙｄｘ＝１
ｄｙ＝ｄｘ
ｙ＋ｃ１＝ｘ＋ｃ２
即ｙ＝ｘ
相当于“ｙ对ｙ取导时，其导数等于１”。
若必有ｙ＝１
（ｌｎｙ）＝１ｙ
——（ｙ＝１）
ｙ是ｘ的函数，ｘ是ｙ的自变量也有
（ｌｎｘ）＝１ｘ
若ｘ是ξ的函数，ξ是ｘ的自变量时（ｘ仍是函数，可导）总也有
（ｌｎξ）＝１ξ等等
（ｙ＝１）中的两式同时存在，称为导数与原函数的相对性质。使用（ｙ
＝１）式可求原函数，也可求导数：
例１
已知ｙ＝ｎｘｎ－１，求ｙ。
令ｙ＝１
ｎｘｎ－１＝１
ｎｘｎ１ｘ＝１
ｎｘｎ（ｌｎｘ）＝１
ｘｎ（ｌｎｘｎ）＝１
则ｙ＝ｘｎ
其中第三步到第四步使用１ｘ＝（ｌｎｘ），
第四步到第五步仍用了同类公式但不同层次１ｙ
=（ｌｎｙ）
例２
已知ｙ＝ｘｎ，求ｙ。
令ｙ＝１
ｘｎ＋１·１ｘ＝１

ｘｎ＋１ｎ＋１（ｎ＋１）（ｌｎｘ）
＝１

ｘｎ＋１ｎ＋１（ｌｎｘｎ＋１）
＝１
求得ｙ＝ｘｎ＋１ｎ＋１（ｙ
＝１）式可以统一为一个式子
ｙ＝１＝ｙ·１ｙ＝ｙ（ｌｎｙ）
即对数求导公式，但这里只是为了求导数。我们的（ｙ＝１）是双向的，可
以用来求原函数。
例３
已知ｙ＝ｕｖ＋ｖｕ，求ｙ。
令ｙ＝１
１＝ｕｖ＋ｖｕ
＝ｕ〔ｖ（ｌｎｖ）〕＋ｖ〔ｕ（ｌｎｕ）〕
＝ｕｖ〔（ｌｎｖ）＋（ｌｎｕ）〕
＝ｕｖ〔ｌｎｖ＋ｌｎｕ〕
＝ｕｖ〔ｌｎｕｖ〕
得ｙ＝ｕｖ
例４
已知ｙ＝ｖｕ－ｕｖｖ２，求ｙ
令ｙ＝１
１＝ｖｕ－ｕｖｖ２
＝ｕｖｕｕ－ｕｖｖｖ
＝ｕｖ（ｌｎｕ）－ｕ
ｖ（ｌｎｖ）
＝ｕｖ〔ｌｎｕｖ〕
得ｙ=ｕｖ
例５
已知ｙ＝ｓｉｎｘ＝１２ｉ
（ｅｉｘ－ｅ－ｉｘ），求ｙ。
令ｙ＝ｙ１－ｙ２
ｙ１＝ｅｉｘ２ｉｙ２
=ｅ－ｉｘ２ｉ
令ｙ′１＝１
＝ｙ１１ｙ１＝ｙ１（ｌｎｙ１
）
＝ｅｉｘ２ｉ｛（ｌｎｅｉｘ
）－（ｌｎ２ｉ）｝
＝ｅｉｘ２ｉ（ｉｘ）
＝ｅｉｘ２
令ｙ′２＝１
＝ｙ２１ｙ２
＝ｙ２（ｌｎｙ２）
＝ｅｉｘ２ｉ｛（ｌｎｅｉｘ
）－（ｌｎ２ｉ）｝
＝ｅｉｘ２ｉ（ｉｘ）
＝ｅｉｘ２
因ｙ＝ｙ′１－ｙ′２
故

ｙ＝ｅｉｘ２－－ｅ－ｉｘ２
＝ｃｏｓｘ
(ｙ＝１）式可用来求原函数，也可用来求导函数。实际上，ｙ＝１的存在
，就是下式的导数
∫ｄｙｙ＝ｌｎｙ＋ｃ
ｄ∫ｄｙｙ＝ｄ（ｌｎｙ）
１ｙ＝ｄｄｙ
（ｌｎｙ）１＝ｙ（ｌｎｙ）








如果ｙ可导，ｙ＝ｆ（ｘ），则
ｙ＝ｙ（ｌｎｙ）
写成ｙ＝１
更为简便。
大家已经知道，以上积分式正是反映自然界多种现象的函数关系模型，因此ｙ
＝１必然与其同价。