庆祝运动论网站成立一周年发表文章 ——微积分的代数根源及其代数化研究(二)

选自《运动论》第283页
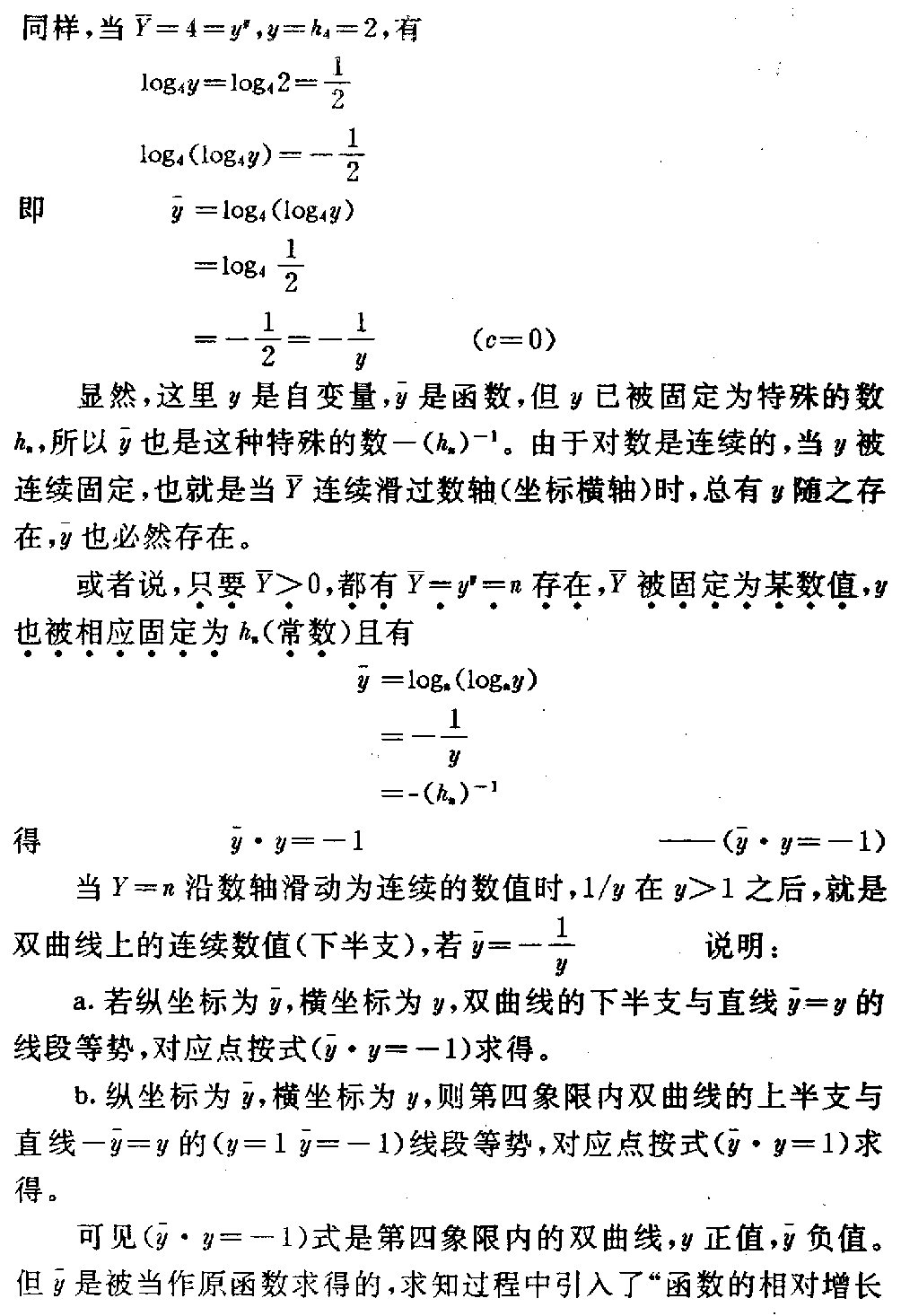
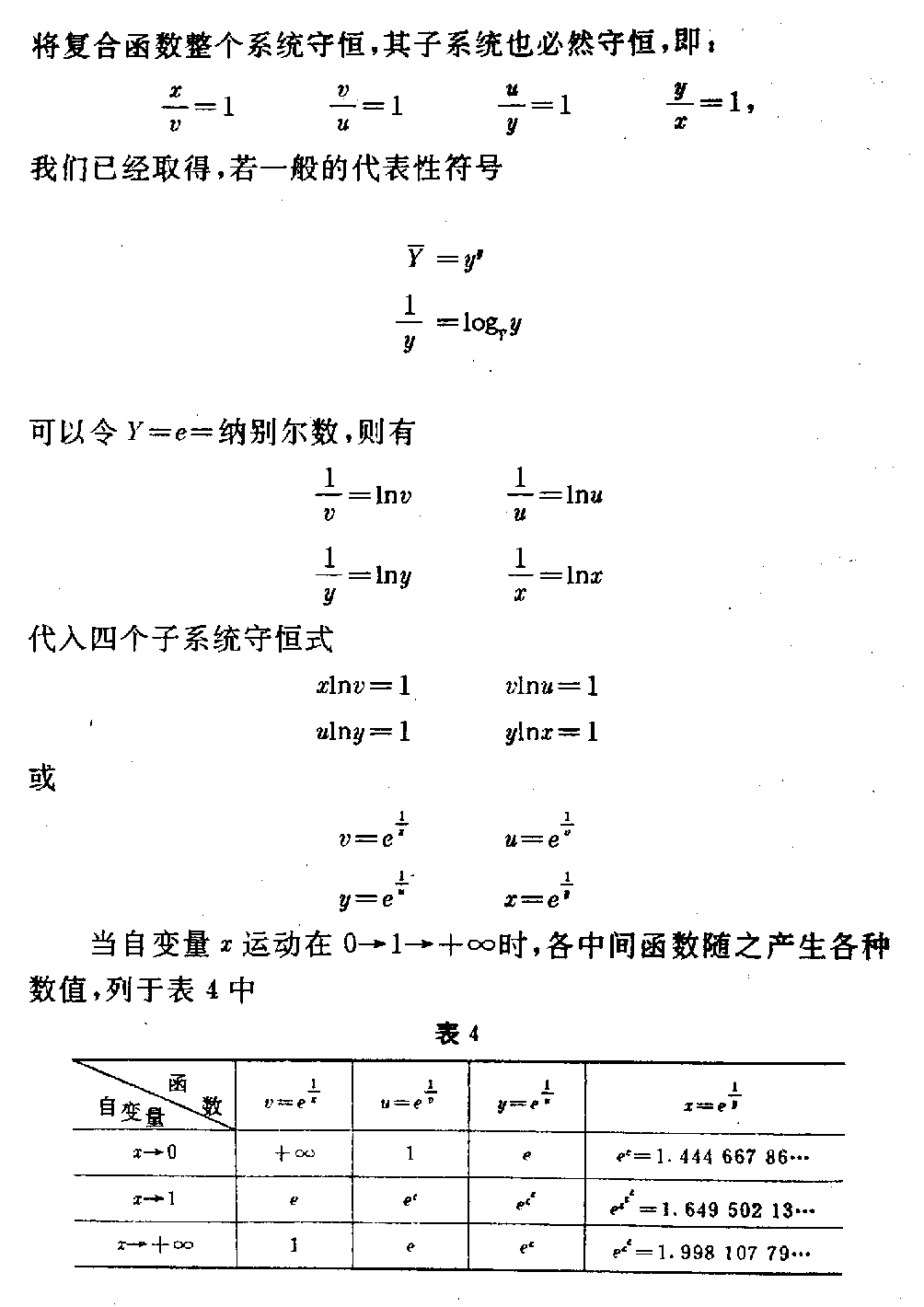
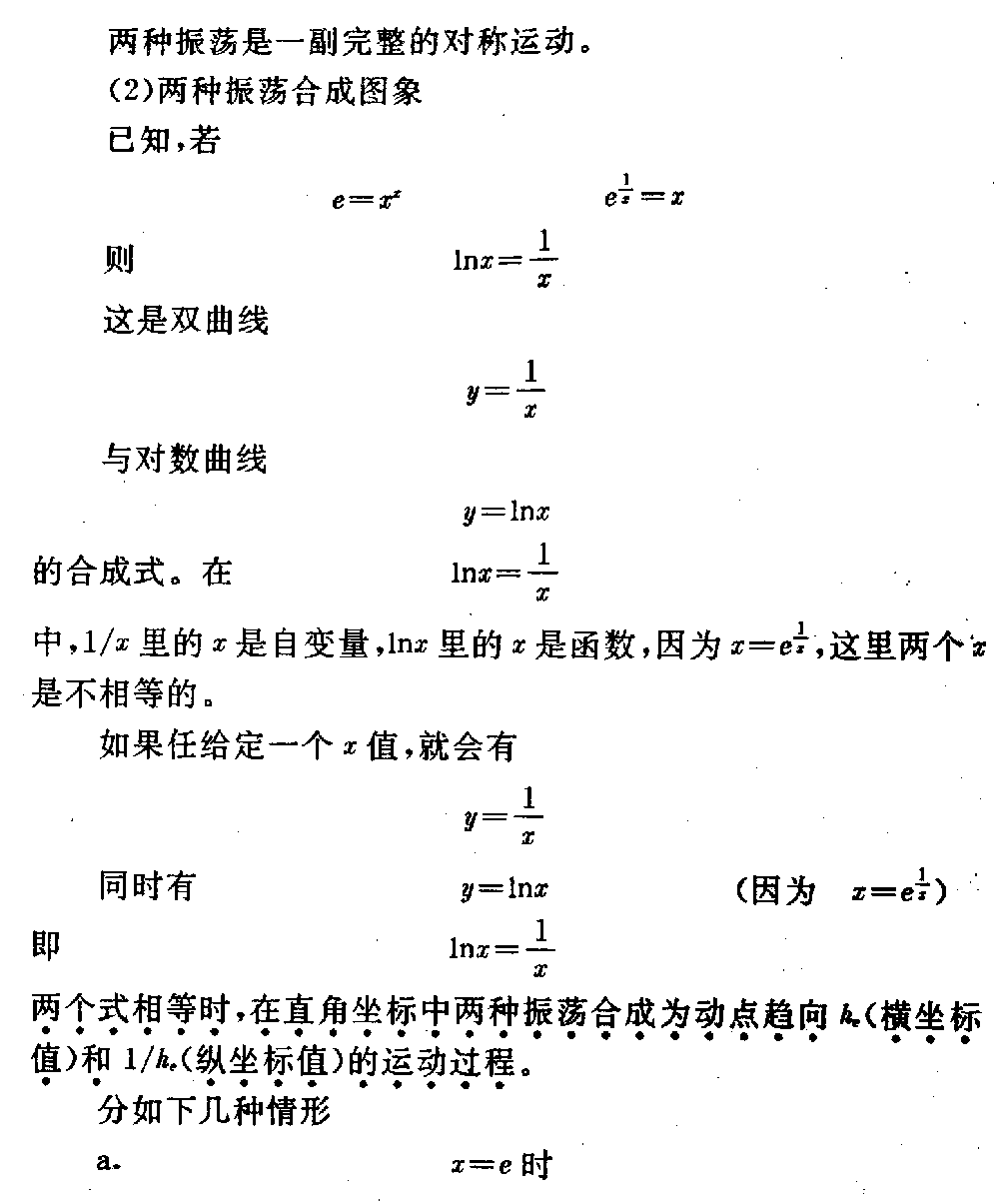
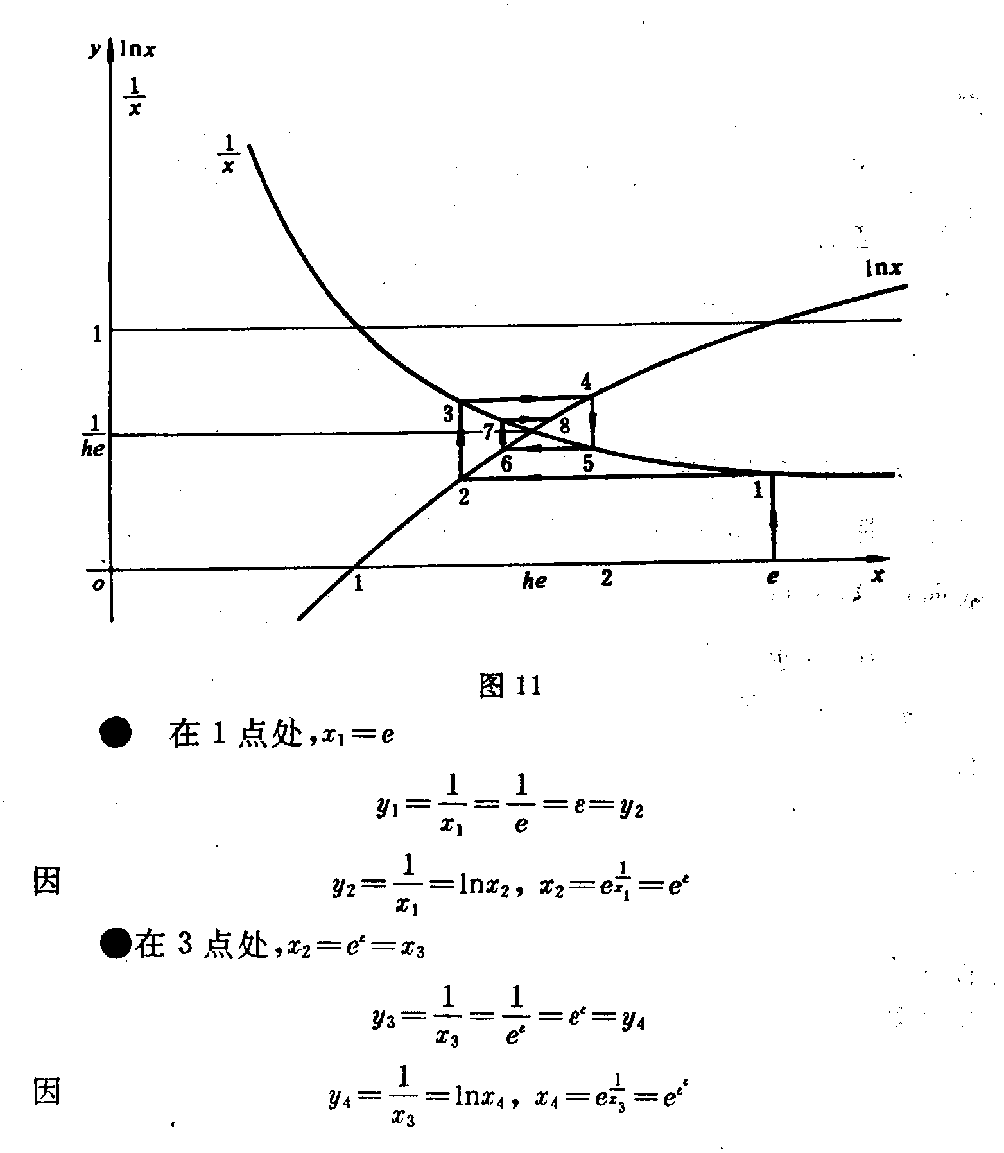
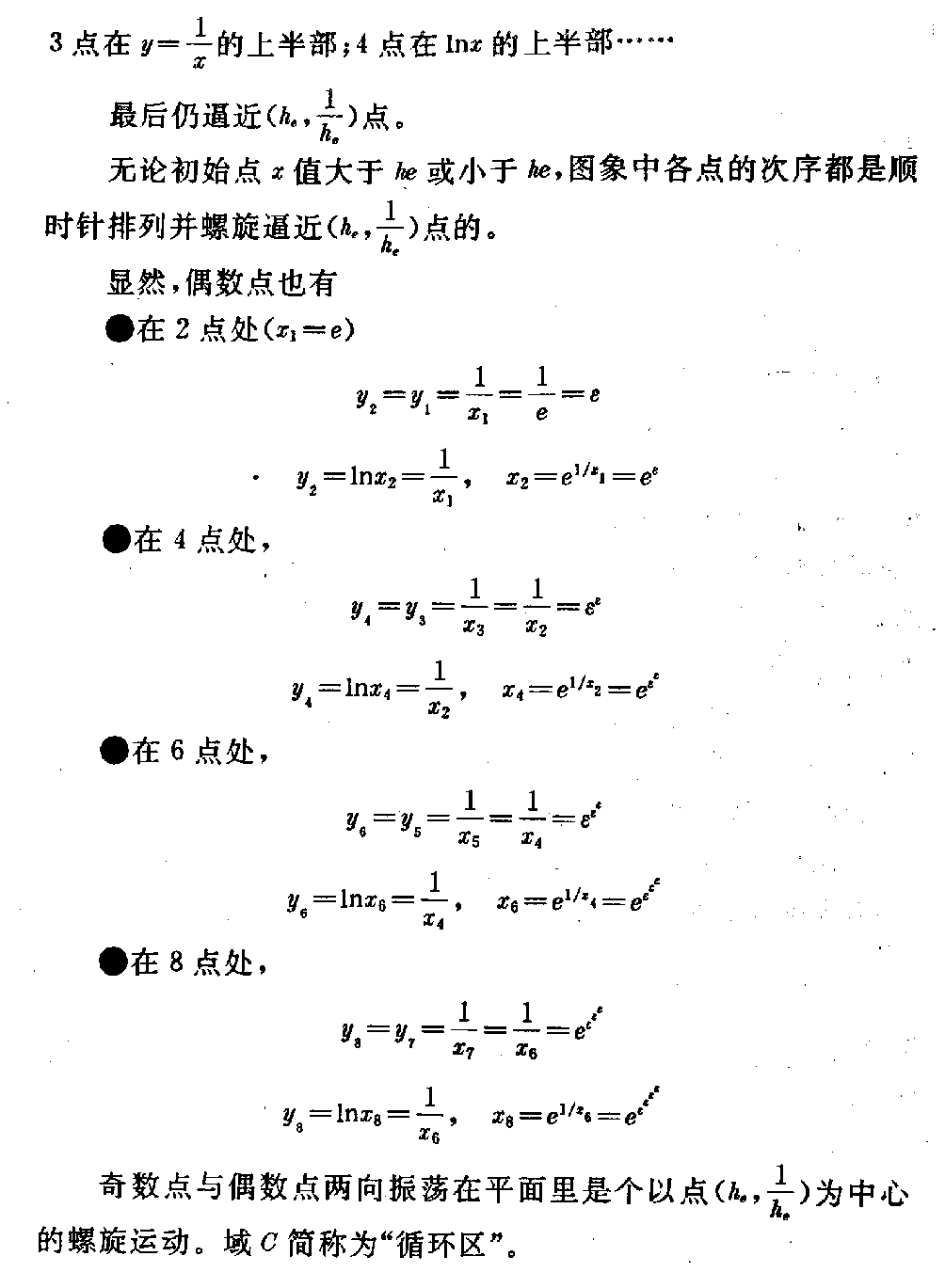
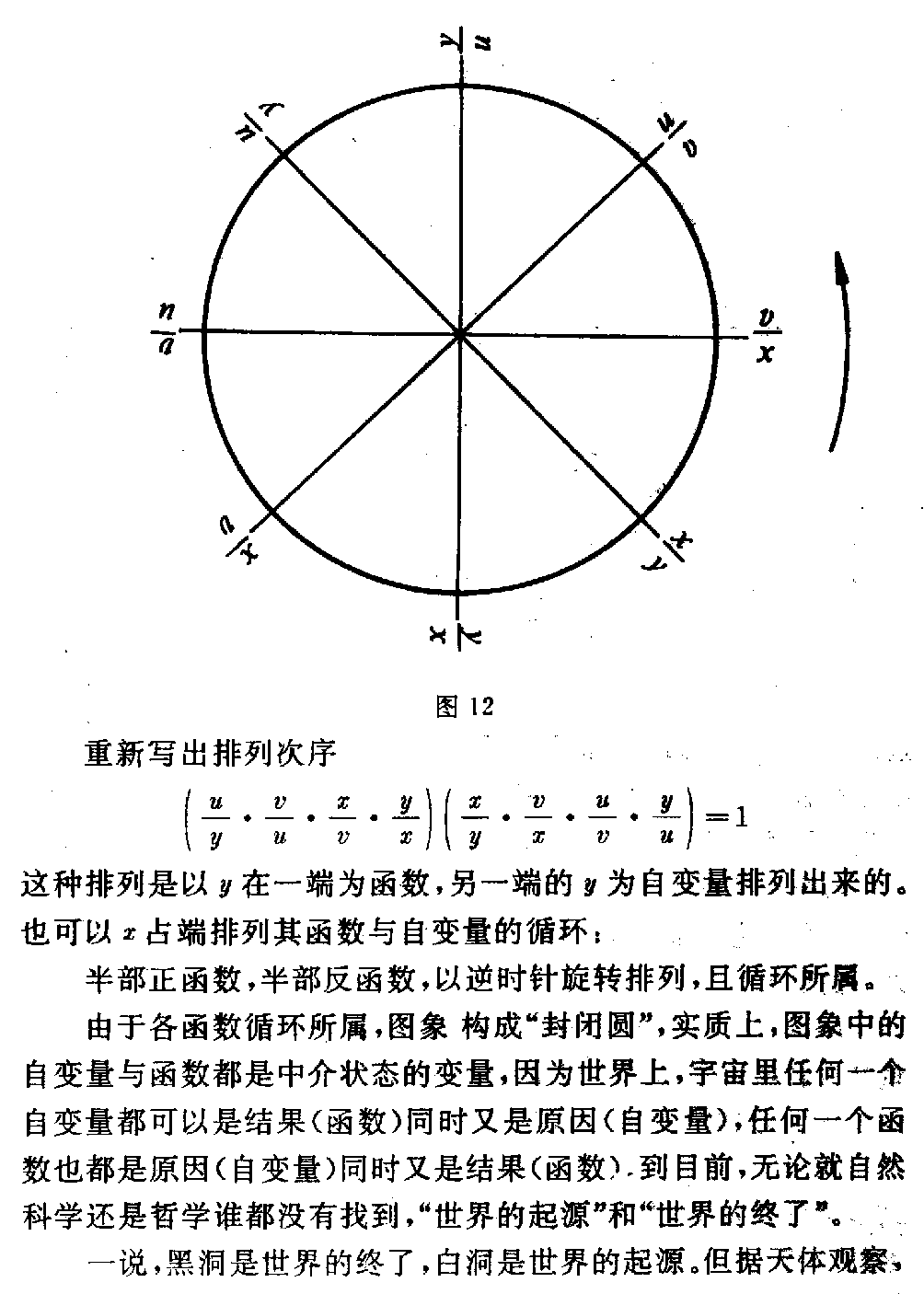
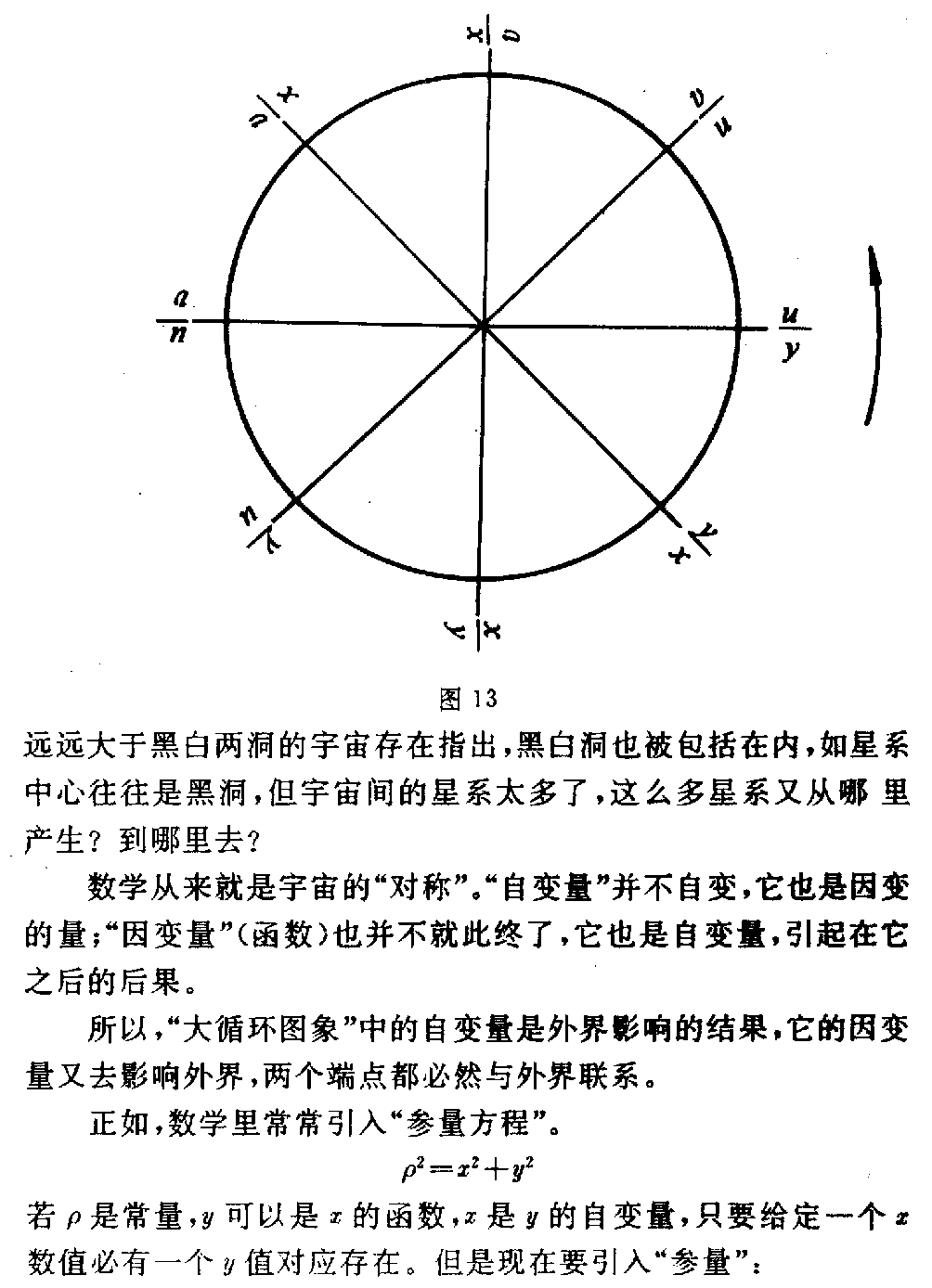
下载
微积分的代数根源及其代数化研究（二）
（一）关于超超越函数
１．超超越函数的几个性质
（１）超超越性
函数Ｆ＝ｘｘ（０＜ｘ≤∞）相似于指数函数，又相似于幂函数，Ｆ的
底数与指数都是同一个ｘ，同步变化。
如，Ｆ被确定为：ｅ（纳别尔数）４，１０，２７…；ｘ也同时被固定为：ｈ，
２，ｈ１０，３…与Ｆ对应。
这里ｈ＝１．７６３２２２８３４…
ｈ１０＝２．５０６１８４１４７…
ｘ从１开始连续运动向无穷大时，Ｆ同时也连续运动向ｘ的ｘ次方延伸向无穷
大，但Ｆ的运动速度比ｘ的运动速度超前ｘ次幂，函数Ｆ的这个性质称为“超
超越性”，称函数Ｆ为“超超越函数”。ｘｘ中的底数Ｘ称为“变量底数”
，指数称为“变量指数”。
（２）极小值
在区间０＜ｘ＜１内，函数Ｆ有极小值。
ｘ→０时，Ｆ→１，
ｘ→１时，Ｆ→１，
其极小值为Ｆ′＝０时的ｘ＝ｘｍｉｎ
Ｆ′＝ｘｘ（ｌｆｘ＋１）＝０
其中
必有ｘｘ≠０（ｌｆｘ
＝ｌｏｇＦｘ）
ｌｆｘ＋１＝０
Ｆ－１＝Ｘｍｉｎ
当Ｆ＝ｅ时，Ｘｍｉｎ＝ｅ－１＝ε
故Ｆｍｉｎ＝εε＝０．６９２  ２００  ６２８…
（３）常量，自变量与因变量的相对性
若Ｆ＝ｅ＝ｘｘ
表成ｘ＝ｅ１ｘ时
——（ｅ１／ｘ）
ｅ１ｘ中的ｘ称为自变量，等于ｘ即为因变
量。
当超超越函数被固定为某一常数后，如
ａ＝ｘｘ
ａ１ｘ＝——
（ａ１／ｘ）
其变量底数ｘ成为函数，变量指数成为自变量，并该新
函数是（ａ１／ｘ）形的指数函数。此时将函数ｘ记为，
显然≠ｘ。
由于Ｆ被固定为常量，引起Ｆ中的变量底数ｘ成为新的函数，变量指数ｘ成为
新的自变量。现在，我们令ａ＝ｅ，并对（ｅ１／ｘ）式取以
ｅ为底的自然对数
ｌｎ＝ｌｎｅ
１ｘ
＝１ｘ
要注意的是此时  ＝ｘ＝ｈ，ｘ与又被固定为常量
ｘ＝ｈ上。若令ｙ＝ｌｎ
变成自变量，ｙ是因变量，有
ｙ·ｘ＝１
此时的ｘ已不是，而是变量指数ｘ成为了自变量。
被埋没在ｌｎ中，以ｙ整体表现出来成为因变量。
对（ｅ１／ｘ）取自然对数，出现
ｘ·ｌｎ＝１
ｘ·ｌｎｅ１ｘ＝１
ｘ·１ｘ＝１
ｘ＝ｘ恒等
由于上述基本过程：对Ｆ函数，（ａ）因定Ｆ为定常数，Ｆ＝ａ＝ｘｘ形中ｘ
也被固定为常数ｈａ；（ｂ）改形为＝ａ１
ｘ，则变成函数，ｘ成为自变量，ｘ离开ｈａ；
（ｃ）取以ａ为底的对数，ｌｏｇａ＝１ｘ，ｘ与又被固定为常数ｈａ；
（ｄ）令ｙ＝ｌｏｇａ，则ｙ·ｘ＝１，ｘ又变成自变量，为中间函数，ｙ成为最后的函数。
但此时ｘ＝１ｙ又出现。
构成一个常量、自变量、因变量的循环运动。这是Ｆ函数的特殊性质。
它要求改变以往对常量、自变量，因变量一成不变的“固有成见”。
（４）守恒性与完整性
出现ｘ＝ｘ
变量的恒等，我们称为“守恒性”。考虑性质（３）该变量守恒的来源知道，这
里的ｘ是开始的变量指数形成的自变量，不是变量底数的守恒。
这说明函数的来源就是守恒的。因此，守恒性将函数的基本存在形式固定下来。
当然也可以任取其一为函数，另一ｘ为自变量进行另一轮的循环
运动：
ｘ＝
ｘ·１＝１
ｘ·ｌｏｇＦ＝１
Ｆ＝ｘ
新的循环在旧的循环运动基础上衔接形成“螺旋扩大的循环”运动，或“螺旋
缩小的循环”运动。
但只有Ｆ不被固定为常量才能形成这种螺旋扩大（缩小）的循环运动。变量的
守恒关系，表现出变量运动的完整性。
因为螺旋扩大（缩小），不断运动（Ｆ不被固定），变量并不守恒，单就一次循环
观察（静止的相对观察）在一次循环内变量又是守恒的，可以建立
ｘ＝ｘ
一般情形应当Ｆ是变量
Ｘ·１＝１
ｌｏｇＦ＝１ｘ
“螺旋”并不准确，乃“变底对数与双曲函数的对等”。我们因为Ｆ的变动，
所以还叫不出它的运动形状。实际上它是个平面。
２．绝对无穷大与相对无穷大的对应关系及其代数变换
康托尔在集合论中说：“部分的元素个数可以等于整体的元素个数”，“任一
线段都与整条线段等势”。
庄子说：“一尺之棰，日取其半，万世不竭”。
他们都是说，有限之内有无限的“元素”、“势”，且可以对等。
反之，既然部分的元素个数与整体的个数相等，所谓“整体”仅与部分的相对
称谓，并未限定“整体”的边界，如果  将“整体”的边界每扩大一次（不
限制扩大多少）都与部分的元素对应一次，按  康托尔的集合论，它们的元素
个数也应相等。当把这种扩大的次数与每次扩大都对应一次元素的个数（总是
相等）无限发展下去，就会得出“无限扩大的整体元素个数与有限的部分元素
个数仍然相等”的结论。
事实上也正是如此，也就是“无限与有限也是等势的”。不乏其例，如：
当１≤ｎ≤∞  时，有
ｎ与１／ｎ是等势的。ｎ无限伸展时，１／ｎ存在于１中，其内的势一一对应
。
当１＜ｎ≤∞，Ｎ＝ｎｎ时，有
ｌｏｇＮｎ与１／ｎ也是等势的。ｎ伸向无穷大，ｌｏｇＮｎ却
限制在１／ｎ中，因为
ｌｏｇＮｎ＝１ｎ
永远成立，１／ｎ就是个相对无穷大，有界无穷大区间。
但是，一旦Ｎ被固定Ｎ＝ｅ、１０等等，ｌｏｇｅｎ、ｌｏｇ１０ｎ
又会超出１／ｎ的界限，伸向绝对无穷大。因为此时Ｎ被固定，保持Ｎ值不变
的ｎ＝ｅ１ｎ或ｎ＝１０１
ｎ能够运动在绝对无穷大区间，其变量指数ｅ１ｎ或１０１ｎ中的ｎ
却向相反方向运动。
上述例中的代数变换就是相对无穷大与绝对无穷大或绝对无穷大与相对无穷
大间的变换。
（１）由给定的“绝对无穷大区间运动”的函数变换为“相对无穷大区间运动
”的函数
双曲函数运动于绝对无穷大区间：
１＝ｘ·ｙ
对ｘ取以ａ为底的对数，并令常量ａ＞１
若ｙ＝ｌｏｇａｘ（０＜ｘ≤∞）
总有＝ａ１ｘ
——（ａ１／ｘ）
＝ａｌｏｇａｘ
＝ｘ
ａ是与ｘ的相对无穷大，与ｘ是存在于特殊相对无
穷大关系（ａ１／ｘ）中的。演进后，这种关系就是变量守恒（恒等）
关系；
＝ｘ
它是封闭式的变量恒等。
（２）由给定的“相对无穷大区间运动”的函数变换为“绝对无穷大区间运动
”的函数。
若给定一个封闭的变量守恒式；
＝ｘ（ｘ自变量，
函数）
总可得＝ａｌｏｇａｘａ＞
１
因为ｌｏｇａｘ＝１ｘ存
在
则ｘ·ｌｏｇａｘ＝１
显然又可·ｙ＝１（ｘ＝）
成为开放型的双曲函数关系。
若只从数学角度看，（１）是由乘法ｘｙ＝１变换为除法·１ｘ＝１（２）是由除法·１ｘ
＝１变换为乘法ｙ＝１。中间借助于ｌｏｇａｘ＝１ｘ
总是存在的关系导来。
那么，由ｘ·１ｘ＝１，ｘ·ｙ＝１  两式直接相
互变来变去，不是也一样可以的吗！
当然可以，但不经过ｌｏｇａｘ＝１ｘ，就看不
到由ｘ＝ｘ到ｙ＝１ｘ，或由ｙ＝１ｘ到ｘ＝ｘ的中间运动过程。可以形象些，从坐标曲线之间看到
＝ｘ（过原点的π／４  角直线）与ｙ＝１ｘ（过（１，１）点的双曲线一支）相互间是通过对数曲线变形达到对
方曲线（或直线）的。
这项变换的重要意义并不在于数学范围上，而是在于封闭的守恒系统与开放的
不守恒系统之间并不横坦一条不可逾越的鸿沟，它们仅仅是一个问题的两个方
面，乃辩证逻辑关系在数学中的表现。反之。我们通过数学证明了辩证关系存
在同一事物中，运动是关键。
这种变换形式尽管很简单，它完全类同圆函数与双曲函数间的变换。
３．超超越函数与一般函数的关系
用下式表示超超越函数
Ｘ＝ｘｘ一般函数用下式表示
ｙ＝ｆ（ｘ）
ｘ是Ｘ与ｙ的“自变量”或称为“原始变量”，“起始变量”。
函数符号ｆ包括任意的加减乘除等等以及微积分运算的运动过程。ｆ（ｘ）是
指一旦有个ｘ的确定值，这个确定值就会经过ｆ内的所有运算过程后达到一个
确定的ｙ值ｙ＝ｆ（ｘ）。但Ｘ却与ｆ（ｘ）大不相同。
可以想像在数轴上，无论给定一个多么大或多么小的ｘ值，与此ｘ给定的同时
，要有两个数出现：（１）Ｘ、（２）μ
Ｘ＝ｘｘ
ｘ＝μμ
Ｘ超前ｘ的ｘ次方；μ迟后ｘ的１／μ次方。
这个现象是超超越函数的特性，是要注意到的。因为它只与给定的ｘ值有关，
与运算过程中的任何ｆ都无关。或者说，Ｘ形式的存在，是概括符号ｆ的一种
“提纯”，显得以往对ｆ的了解和认识中，已有这种“指数函数”（苏联科学
院院士鲁金的《微分学》把这种函数当作指数函
数），但又未精炼这种函数的极为特殊的性质，经过“提纯”达到对它的“超
超越性”上面来。
与此同时，产生的“数”还不光有Ｘ、μ，而是一系列的“数”向两个方向发展
μ＝γγ
γ＝ξξ
……
直至极小值ω→０。
Ｗ＝ＸＸ
Ｖ＝ＷＷ
……
直至极大值Ａ→∞
这些数值在ｘ为一个确定数值时，跳跃在整个数轴上，但是也有特殊点：
ｌｉｍω→０ωω＝１
ｌｉｍｘ→１ｘｘ＝１
ｌｉｍＡ→∞ＡＡ＝∞
（１ｅ）（１ｅ）＝０．６９２  ２００  ６２８…
ｅ为纳别尔数
现在我们看看Ｘ与ｙ＝ｆ（ｘ）是什么关系。作如下处理：
ｘ＝Ｘ１／ｘ
Ｘ〔１Ｘ１／ｘ〕
＝Ｘ〔１Ｘ〕１／ｘ
＝Ｘ〔１Ｘ
）〔１Ｘ）１／ｘ＝…
因为每个ｘ都可以写为Ｘ的１／ｘ次方，所以上式的Ｘ指数将会无限以１／Ｘ写
下去。我们将它简记作
ｘ＝Ｘ（１ｘ）
∞↑——
（１ｘ）∞↑
〔对于μμ＝ｘ
也有类似的情况
μ＝ｘ１／μ＝ｘ（
１ｘ）１／μ＝…＝ｘ
（１ｘ）
∞↑
——（μ）
暂将（μ）式从略。〕
因此，若ｙ＝ｆ（ｘ）的反函数是ｘ＝φ（ｙ）
便会得到
ｘ＝Ｘ（１ｘ）∞↑＝φ（ｙ）——（ｘ→Ｘ→ｙ）
（ｘ→Ｘ→ｙ）式指明：
“函数关系符号φ可以〔Ｘ（
１ｘ）∞↑〕形式的无限次人为的手续代替，其中Ｘ＝ｙ”，或
ｙ＝ｘｘ（ｘ＞０）
于是，Ｘ＝ｘｘ＝ｙ又代替了正函数符号ｆ。
果真可将复杂的函数关系ｆ用ｘｘ取代吗？如果我们将ｙ＝ｆ（ｘ）看成一
个系统，前一小节介绍的“变量守恒原理”也可成为“系统守恒原理”。无论
ｙ＝ｆ（ｘ）是守恒的或不恒的，都可以相互变换，取而代之的ｙ＝ｘｘ是
个守恒式被得证时，这种变量代换也就存在了，但并不唯一。这就是
若ｙ＝ｘｘ
则ｙ（１ｘ）＝ｘ
有ｌｏｇｙｘ＝１ｘ
用对数换底公式，习惯于取ｅ为底数，有
ｘ·ｌｎｘｌｎｙ＝１
ｘ·ｌｎｘｌｎｘｘ＝１
ｘ·ｌｎｘｘ·ｌｎｘ＝１
１＝１
或ｘ＝ｘ
守恒。
ｙ＝ｆ（ｘ）为任意形式的函数。当ｙ＝ｆ（ｘ）被ｙ＝ｘｘ代
换后，仍然保持原始自变量ｘ的守恒存在，无论中间运动过程怎样ｆ，量ｘ并
不丢失。但途径改变了。
又因为一旦建立
ｙ＝ｘｘ时
就会同时有
Ｙ＝ｙｙ产生。
我们知道，函数的相对增长率被定义为ｙ／ｙ
ｙｙ　＝（ｌｎｙ）
这里ｙ＝ｄｄｘｙ（ｌｎｙ）
＝ｄｄｘｌｎｙｙ＝ｆ（ｘ）
故ｄｙｄｘ
ｙ＝ｄｄｘｌｎｙ
ｄｙｙ＝ｄ（ｌｎｙ）
１ｙ＝ｄｄ
ｙ（ｌｎｙ）
指明，函数的对数对自身取导数时，其相对增长率等于函数的倒数。这个结果
恰恰是
Ｙ１ｙ＝ｙ
ｌｏｇＹｙ＝１ｙ
从这里又得证，当ｙ＝ｘｘ存在时，必同时有Ｙ＝ｙｙ
产生，且导数ｙ＝ｄｙｄｙ＝１
ｙ＝ｄｙｄｘ
存在，因而ｙ＝ｘｘ能够取代ｙ＝ｆ（ｘ）。
上结果中，有几个副产品
（１）Ｙ＝ｅ，ｙ→ｈ＝１．７６３  ２２２  ８３４…
（２）ｌｎｙ＝１ｙ＝ｄｄ
ｙ（ｌｎｙ）
则ｄｙ＝ｄ（ｌｎｙ）
ｌｎｙ
＝ｄ〔ｌｎ（ｌｎｙ）〕
若ｙ＝ｆ（ｘ）  则ｙ对ｘ的导数
ｄｙｄｘ＝
ｄｄｘ〔ｌｎ（ｌｎｙ）〕
反推＝１ｌｎｙ
ｄ（ｌｎｙ）ｄｘ
＝ｄｙｙ·ｌｎｙ·ｄｘ

因ｙ·ｌｎｙ＝ｌｎｙｙｅ＝ｙｙ
ｄｙｄｘ
＝ｄｙｌｎｙｙ·ｄｘ
＝ｄｙｄｘ
或表示成
ｄｙｄｘ＝
ｄｄｘ〔ｌｎ（ｌｎｙ）〕
ｄｙ＝ｄ〔ｌｎ（ｌｎｙ）〕
积分＝ｌｎｌｎｙ＋ｃ
这就是说，当Ｙ＝ｅ，ｙ被固定ｙｙ＝ｅ，ｙ＝ｈ＝１．７６３  ２２２  
８３４…时，有
ｌｎｈ＝０．５６７１４３２８９…

＝ｌｎｌｎｈ＝－０．５６７１４３２
８９…
＝－ｈ－１（ｃ＝０）
同理，当Ｙ＝１０＝ｙｙ，ｙ＝ｈ１０＝２
５０６　１８４　１４７…时，有
ｌｇｈ１０＝０．３９９  ０１２  ９７８…
ｌｇｌｇｈ１０＝－０．３９９  ０１２  ９７８…
＝－（ｈ１０）－１
同样，当＝４＝ｙｙ，ｙ＝ｈ４＝２，有
ｌｏｇ４ｙ＝ｌｏｇ４２＝１２
ｌｏｇ４（ｌｏｇ４ｙ）＝－１２
即＝ｌｏｇ４（ｌｏｇ４ｙ）
＝ｌｏｇ４１２
＝－１２＝－１ｙ
（ｃ＝０）
显然，这里ｙ是自变量，是函数，但ｙ已被固定为特殊的数ｈ
ｎ，所以也是这种特殊的数－（ｈｎ）－１。由于对数
是连续的，当ｙ被连续固定，也就是当连续滑过数轴（坐标横轴
）时，总有ｙ随之存在，也必然存在。
或者说，只要＞０，都有＝ｙｙ＝ｎ
存在，被固定为某数
值，ｙ也被相应固定为ｈｎ（常数）且有
＝ｌｏｇｎ（ｌｏｇｎｙ）
＝－１ｙ
＝（ｈｎ）－１
得·ｙ＝－１——（·ｙ＝－１）
当Ｙ＝ｎ沿数轴滑动为连续的数值时，１／ｙ在ｙ＞１之后，就是双曲线上的
连续数值（下半支），若＝－１ｙ
说明：
ａ．若纵坐标为，横坐标为ｙ，双曲线的下
半支与直线＝ｙ的线段等势,对应点按式（·ｙ＝－１）
求得。
ｂ．纵坐标为，横坐标为ｙ，则第四象限内双曲线的上半支与
直线－＝ｙ的（ｙ＝１  ＝－１）线段等势，对应
点按式（·ｙ＝１）求得。
可见（·ｙ＝－１）式是第四象限内的双曲线，ｙ正值，负值。但是被当作原函数求得的,求知过程中引入了“函数
的相对增长率ｙ／ｙ等于函数的对数ｌｎｙ之导数（ｌｎｙ）”
公式。就这一事件本身，出现的结果是很耐人寻味的。
４．超超越函数与复合函数的关系
复合函数ｙ＝Ｆ（ｕ）
ｕ＝φ（ｖ）ｖ＝ｆ（ｘ）
ｘ是自变量，ｕ、ｖ是中间函数，可写成
ｙ＝Ｆ〔φ｛ｆ（ｘ）｝〕
这个式子与
ｙ＝ｙ（ｘ）
的属性是没有区别的，区别的只是指令的阶段符号，将任意一个函数ｙ（ｘ）
内的各种运算用所属关系的阶段符号表示出来而已。所以还可写成
ｙ＝Ｆ（ｘ）
也可以说，将Ｆ（ｘ）式以复合函数形式表达能使人看到函数内运动的各阶段
变化。比较前节“超超越函数与一般函数的关系”更清晰看到一个函数内部如
何运动过程。那里我们得到“函数关系符号φ可以Ｘ
（１ｘ）∞↑
形式的无限次人
为的手续代替，其中Ｘ＝ｙ”，“若ｙ＝Ｘ＝ｘｘ，将保持原始自变量ｘ的
变量守恒”。
对于复合函数也同样必然是变量守恒的：
设自变量ｘ＞０，
守恒式ｘ＝ｘ
ｘ·１ｘ＝１
若复合函数内的中间函数应用“链锁律”插入原始变量守恒式中
ｘｖ·ｖｕ·
ｕｙ·ｙｘ＝１
将复合函数整个系统守恒，其子系统也必然守恒，即：
ｘｖ＝１ｖｕ＝１ｕｙ＝１ｙｘ＝１，
我们已经取得，若一般的代表性符号
＝ｙｙ
１ｙ＝ｌｏｇ
ｙ
可以令Ｙ＝ｅ＝纳别尔数，则有
１ｖ＝ｌｎｖ１
ｕ＝ｌｎｕ
１ｙ＝ｌｎｙ１ｘ＝ｌｎｘ
代入四个子系统守恒式
ｘｌｎｖ＝１ｖｌｎｕ＝１
ｕｌｎｙ＝１ｙｌｎｘ＝１
或
ｖ＝ｅ１ｘ
ｕ＝ｅ１ｖ
ｙ＝ｅ１ｕｘ＝ｅ
１ｙ
当自变量ｘ运动在０→１→＋∞时，各中间函数随之产生各种数值，列于表４中
表４

自变量函数ｖ
＝ｅ１ｘｕ＝ｅ１ｖｙ＝ｅ１ｕｘ＝ｅ
１ｙ
ｘ→０＋∞１ｅｅε＝１．４
４４  ６６７  ８６…ｘ→１ｅｅεｅεεｅεεε＝１．６４９  ５０２  １３…ｘ→＋∞
１ｅｅεｅεε＝１．９９８  １０７  ７９…
其中，ε＝１ｅ，ｅ＝２．７１８  ２８１  ８２
８  ４５９  ０４５…
可以看到如下运动规律：
当自变量ｘ运动在１≤ｘ≤＋∞时
（１）函数ｘ＝ｅ１ｙ
运动在ｙ的ｅε≤ｙ
≤ｅεε区间内，但与ｙ的运动方向相反。
（２）函数ｙ＝ｅ１ｕ运动在ｕ的
ｅε≤ｕ≤ｅ区间内，但与ｕ的运动方向相反。
（３）函数ｕ＝ｅ１ｖ运动在ｖ的１
≤ｖ≤ｅ区间内，但与ｖ的运动方向相反。
（４）函数ｖ＝ｅ１ｘ运动在自变量
ｘ的１≤ｘ≤＋∞区间内，但与ｘ的运动方向相反。
表４中，我们仅将复合函数以五级中间变量为例的情形，它们是自变量
ｘ级、中间函数ｖ级，中间函数ｕ级，中间函数ｙ级、函数ｘ级。
从（１）→（４）的运动过程清楚地看到：
●由于ｘ的运动，引起共五级变量的“往复阻尼振荡”。它们都是一级所属
一级的往下传递运动，每一级迟后１８０°角。且振幅越来越小，形成一种“
阻尼振荡”现象。
由于开始我们仅仅以“单纯数学方法”进行的“纯数学研究”，至此竟引出在
“纯数学”中的自然现象（阻尼振荡），不能不使笔者大惊！这一结果告知我
们：“变量守恒运动与阻尼减幅振荡相吻合”。
这是一个很具实际应用价值的结果，其发展前景很使人乐观。
●“阻尼振荡”最后使函数ｘ趋近于定值ｈ
ｘ→ｈ＝１．７６３  ２２２  ８３４…
这里ｅ＝ｈｈ
实际上，ｈ不是“定值”，它是个永无休止的比数“ｅ”更加“无理”的无理数
。相对而言，它与“１”比较，是向小的方向无限延伸的一种特定的运动，这
个特定的运动是由
ｅ＝ｈｈ
决定的。
一般情形中，每一个值都有
Ｘ＝ｘｘ
和
ｘ＝μμ
以及Ｘ的超超越增长，μ的超超越减小两向运动乃至无穷。
●复合函数比单函数ｙ＝ｆ（ｘ）更清楚地看到，它们在“变量守恒”的运
动中，无论ｆ或Ｆ是什么形式，变量ｘ的运动都趋向“定值ｈｎ，Ｆ与ｆ只
决定ｘ的运动路线。
●由自变量ｘ的运动，促使函数ｘ趋近“定值”可以人为的“无限次代入的
手续”取得，即按式
ｘ＝Ｘ１ｘ∞↑
取得。
对于任意函数ｙ＝ｆ（ｘ），存在有ｘ→ｈｎ，且ｈｎ是唯一的“定数值
”，我们就称函数ｙ是“单源”的函数。到现在，我们
还不知道存在“非单源”的函数是怎样的函数（ｘ＝０除外），比如，不是连
续的函数可能就是“非单源”的。
●函数ｘ的谐振区在ｙ的（ｅε，ｅεε）内，方向相反，ｙ是
ｘ的原因，ｘ∈ｙ；
ｙ的谐振区在ｕ的（ｅ，ｅε）内，方向相反，ｕ是ｙ的原因，ｙ∈ｕ；
ｕ的谐振区在ｖ的〔１，ｅ）内，方向相反，ｖ是ｕ的原因，ｕ∈ｖ；
ｖ的谐振区在ｘ的〔１，＋∞）内，方向相反，ｘ是ｖ的原因ｖ∈ｘ（自
变量）。
有函数ｘ∈ｙ∈ｕ∈ｖ∈ｘ自变量。
这是个逐层所属，又是个循环所属的关系。
这是个新出现的怪圈。它以守恒原理建立，以阻尼的衰减谐振荡形式运动，以
原因ｘ开始，以结果仍然是ｘ告终。并且只要原因ｘ有一个任意大小的振源（
给定Ｘ＝ｘｘ值）都将使结果ｘ趋向一个定值，这个定值决定于Ｘ振源的具体
数值，使结果ｘ＝Ｘ１ｘ＝Ａ１ｘ（Ａ为一个确定的数，此时Ａ＝Ｘ）。
５．方法与观念的统一科学方法与自然观，
世界观是统一的观点早已为人们认识并接受。
我这里说的方法，不仅是具体的数学方法而且这一数学方法本身自带有“伸展的
阶段性”、“完整的系统性”、“变量的守恒性”、“运动的谐振性”、“方
法的根本性”，这些性质体现了反映客观观念的一致。
（１）前小节已经得到，若一个函数ｙ＝ｆ（ｘ），必存在反函数ｘ＝φ（ｙ
），ｘ是正函数ｙ的自变量，任一自变量总有X＝ｘｘ，ｘ＝μμ存在（
ｘ＞０），因此
ｘ＝Ｘ（１ｘ）∞
↑
＝φ（ｙ）完整性
获ｙ＝Ｘ
＝ｘｘ
或ｘ＝Ｘ１ｘ
ｌｏｇＸｘ＝１ｘ
当Ｘ＝ｅ
ｘ·ｌｎｘｌｎＸ＝１
ｘ＝ｘｘ·１ｘ＝１
守恒性
（参看“３．超超越函数与一般函数的关系”）
当Ｘ＝ｅ时，还可得：
ｘ＝ｅ１ｘ
现在，把此式等号两边的函数与ｅ１ｘ拉开
，填进中间函数，立即就变成一个复合函数
ｘ＝ｅ１ｙ，ｙ＝ｅ
１ｕ，ｕ＝ｅ１
ｖ，ｖ＝ｅ１
ｘ阶段性
也可以代入形式写出
ｘ＝ｅ１ｙ
＝ｅε１ｕ
＝ｅεε１ｖ
＝ｅεεε１ｘ
系统性
同一函数的几个表示方法已经体现出完整性、守恒性、阶段性、系统性。
现在仍对
ｘ＝ｅ１ｘ
——（５－１）
第一步取倒数，仍然相等，有
１ｘ＝１ｅ１ｘ＝ε１ｘ——（５－２）
第二步以等式为ｅ的指数，仍相等
ｅ１ｘ＝ｅε１
ｘ——（５－３）
重复第一步，取倒数
１ｅ１ｘ＝εε１ｘ——
（５－４）
重复第二步，
ｅε１ｘ＝ｅεε
１ｘ——（５－５）
无限次重复一二两步骤，就会有奇数次步骤完了的结果是
εεε…１ｘ
∞＝１ｈｅ
＝０．５６７  １４３  ２９…
偶数次步骤完了的结果是
ｅεε…１ｘ
∞＝ｈｅ
＝１．  ７６３  ２２２  ８３４…整个运动过程是一
个“逐渐  衰减的阻尼谐振荡”，最后趋向定值ｈｅ与ｈ
－１ｅ。且
ｈｅ×１ｈｅ＝１
奇数次结果乘偶数次结果等于１。
前述的“４．超超越函数与复合函数的关系”所列各中间函数的数表数，只是
这里的各阶段偶数次步骤结果。或者“４”的数表数只是这里运动过程的一个
片面。我们说，新方法充分体现了概念，方法本身具有根本性。
我们看到，每取两个步骤，等于填进一个中间函数。这说明“人为的取步骤手
续可以取代中间函数”，这是一个异常积极的结果，结果告知我们，客观的某
种运动ｙ＝ｆ（ｘ）可以人的恰当行为取代；人类能够介入客观的某种运动并
有主宰作用，使之人为再现。
因此，偶数步骤是“４（数表）”的一种阻尼谐振，那么奇数步骤
各阶段数也是一种振荡，若自变量ｘ运动在
０＜ｘ≤＋∞
则函数ｘ→１ｈｅ＝０．５６７  １４
３２９…
两种振荡是一副完整的对称运动。
（２）两种振荡合成图象
已知，若
ｅ＝ｘｘｅ１ｘ
＝ｘ
则ｌｎｘ＝１ｘ
这是双曲线
ｙ＝１ｘ
与对数曲线
ｙ＝ｌｎｘ
的合成式。在ｌｎｘ＝１ｘ
中，１／ｘ里的ｘ是自变量，ｌｎｘ里的ｘ是函数，因为ｘ＝ｅ１ｘ，这里两个ｘ是不相等的。
如果任给定一个ｘ值，就会有
ｙ＝１ｘ
同时有ｙ＝ｌｎｘ（因为ｘ＝ｅ
１ｘ）
即ｌｎｘ＝１ｘ
两个式相等时，在直角坐标中两种振荡合成为动点趋向ｈｅ（横
坐标值）和１／ｈｅ（纵坐标值）的运动过程。
分如下几种情形
ａ．ｘ＝ｅ时
图１１
●在１点处，ｘ１＝ｅ
ｙ１＝１ｘ１＝１ｅ＝ε＝ｙ２
因ｙ２＝１ｘ１＝ｌｎｘ２
，　ｘ２＝ｅ１ｘ１＝ｅε
●在３点处，ｘ２＝ｅε＝ｘ３
ｙ３＝１ｘ３＝１ｅ
ε＝εε＝ｙ４
因ｙ４＝１ｘ３＝ｌｎｘ４
，　ｘ４＝ｅ１ｘ３＝ｅεε
●在５点处，ｘ４＝ｘ５
ｙ５＝１ｘ５＝εεε＝
ｙ６
因ｙ６＝１ｘ５＝ｌｎｘ６
，　ｘ６＝ｅ１ｘ５＝ｅεεε
●在７点处，ｘ６＝ｘ７
ｙ７＝１ｘ７＝１ｘ
６＝εεεε＝ｙ８
因ｙ８＝１ｘ７＝ｌｎｘ８
，　ｘ８＝ｅ１ｘ７＝ｅεε
εε
继续无限次求下去，图象上的奇数点就会逼近（ｘｎ，ｙｎ）＝（ｈｅ
，１ｈｅ）点，这里
ｌｉｍｎ→∞ｘｎ＝ｈｅ＝１．
７６３  ２２２  ８３４…
ｌｉｍｎ→∞ｙｎ＝１
ｈｅ＝０．５６７  １４３  ２９…
从图象中可以清楚地看到，这是个以点（ｈｅ，１ｈｅ）为中心的“阻尼衰减振荡”运动，从点１振到点３，又从点３振到点
５，…最后无限逼近中心点（ｈｅ，１ｈｅ
）。
现在，要求在这里必须重复说明一件事：
我们说，任给一个ｘ自变量的值，都存在
有
Ｘ＝ｘｘ
和
ｘ＝μμ
存在。
当函数ｙ＝ｆ（ｘ）时，总有反函数
ｘ＝φ（ｙ）
＝Ｘ１ｘ
因此，任意函数形式φ被Ｘ１ｘ所代替，并有
ｙ＝Ｘ
〔ｘ＝Ｘ（１Ｘ）
１ｘ＝Ｘ（
１ｘ）↑∞〕
当Ｘ被确定为某值，如Ｘ＝ｅ时，则
ｌｏｇＸｘ＝ｌｎｘ＝１ｘ
Ｘ不被确定为定值时，有
ｌｏｇＸｘ＝（ｌｎｘ）＝１ｘ
请注意这个等式中，是与ｘ之自然对数的导数连在一起的。这就是“数学分析
”所说的“函数ｙ＝ｆ（ｘ）在（ｘ＝ｈｎ的）域Ｃ是解析的，单
源的，或单演的”。简而言之，“函数ｙ＝ｆ（ｘ）源
于ｈｎ点，域Ｃ由初始条件ｘ的初值决定”。
如果ｅ是纳别尔数，这个域Ｃ恰好在图象的１、２、３、４点围定的域之内。
因此，X被确定为ｅ，是“数学分析”的基础数，那么它的运动域Ｃ也是可以
具体确知的，而不是抽象的。
“函数ｙ＝ｆ（ｘ）源于ｈｎ点”包含着导数（ｌｎｘ）存在。因为
永远有“相对无穷大区间”
（ｌｎｘ）＝１ｘ=ｌｏｇＸｘ
存在，所以就不必（ｌｎｘ）之麻烦阐述，这是微分代数化
的根源和路径参看本文３．超超越函
数与一般函数的关系。。
ｂ．ｘ＜１时，
１点在ｙ＝１ｘ双曲线的上半部；２点在对数ｌ
ｎｘ曲线的上半部；３点在ｙ＝１ｘ的下半部；
４点在ｌｎｘ的下半部……
最后仍逼近（ｈｅ，１ｈｅ）点。
无论初始点ｘ值大于ｈｅ或小于ｈｅ
，图象中各点的次序都是顺时针排列并螺旋逼
近（ｈｅ，１ｈｅ）点的。
显然，偶数点也有●在２点处（ｘ１＝ｅ）
ｙ２＝ｙ１＝１ｘ１＝
１ｅ＝ε
ｙ２＝ｌｎｘ２＝１ｘ１
，ｘ２＝ｅ１／ｘ１＝ｅε
●在４点处，
ｙ４＝ｙ３＝１ｘ３＝
１ｘ２＝εε
ｙ４＝ｌｎｘ４＝１ｘ２
，ｘ４＝ｅ１／ｘ２＝ｅεε
●在６点处，
ｙ６＝ｙ５＝１ｘ５＝
１ｘ４＝εεε
ｙ６＝ｌｎｘ６＝１ｘ４
，ｘ６＝ｅ１／ｘ４＝ｅεεε
●在８点处，
ｙ８＝ｙ７＝１ｘ７＝

１ｘ
６＝ｅεεε
ｙ８＝ｌｎｘ８＝１ｘ６
，ｘ８＝ｅ１／ｘ６＝ｅεε
εε
奇数点与偶数点两向振荡在平面里是个以点（ｈｅ，１ｈ
ｅ）为中心的螺旋运动。域Ｃ简称为“循环区”。
６．“大循环图象”
若复合函数
ｙ＝Ｆ（ｕ）
ｕ＝φ（ｖ）
ｖ＝ｆ（ｘ）
ｘ＝Ｚ（ｙ）
它的反函数总可记为：
ｕ＝Ｐ（ｙ）
ｖ＝Ｑ（ｕ）
ｘ＝Ｒ（ｖ）
ｙ＝Ｗ（ｘ）
对正函数有变量守恒：产生一个ｘ，必有超超越函数
X＝ｘｘ
则ｘ·ｌｏｇXｘ＝１
ｘ·ｌｏｇａｘｌｏｇａX＝１
ｘ·ｌｏｇａｘｘ·ｌｏｇａｘ＝１
ｘ＝ｘ守恒式
同样，其反函数也有变量守恒：产生一个ｙ，必有超超越函数
Ｙ＝ｙｙ
则ｙ·ｌｏｇＹｙ＝１
ｙ·ｌｏｇａｙｌｏｇａＹ＝１
ｙ·ｌｏｇａｙｙ·ｌｏｇａｙ＝１
ｙ＝ｙ守恒式
根据键锁律，插入中间函数
ｙｕ·ｕｖ·ｖｘ·ｘｙ＝１
其中
１ｕ＝ｌｎｕｙｌｎｕ
＝１ｕ＝ｅ１ｙ
１ｖ＝ｌｎｖｕｌｎｖ
＝１ｖ＝ｅ１ｕ
１ｘ＝ｌｎｘｖｌｎｘ
＝１ｘ＝ｅ１ｖ
１ｙ＝ｌｎｙｘｌｎｙ
＝１ｙ＝ｅ１ｘ
这诸公式与正函数类同，但此时
ｙ→ｈｅ
借助于“４．超超越函数与复合函数的关系”，重要的是我们又得到：
ｘｖ·ｖｕ
·ｕｙ·ｙｘｙｕ·ｕｖ·ｖｘ·ｘｙ＝１
正函数与反函数共同守恒。
在正函数的数表中，我们得到：
函数ｘ∈ｙ∈ｕ∈ｖ∈ｘ自变量；自然在反函数中也有：
函数ｙ∈ｘ∈ｖ∈ｕ∈ｙ自变量。
一反一正两种循环所属的关系共同组成一个循环。因此，我们可以４个变量的
复合函数正反函数组成的共８个除法关系布置在一周上。当然，复合函数的中
间函数不拘一格，是多种多样的，因此也不只限于４个变量。我们现在只作出
４个变量的“大循环”图，可以吻合一种物理模型。
图１２
重新写出排列次序
ｕｙ·ｖｕ
·ｘｖ·ｙｘｘｙ·ｖｘ·ｕｖ·ｙｕ＝１
这种排列是以ｙ在一端为函数，另一端的ｙ为自变量排列出来的。也可以ｘ占
端排列其函数与自变量的循环：
半部正函数，半部反函数，以逆时针旋转排列，且循环所属。
图１３

由于各函数循环所属，图象  构成“封闭圆”，实质上，图象中的自变量与
函数都是中介状态的变量，因为世界上，宇宙里任何一个自变量都可以是结果
（函数）同时又是原因（自变量），任何一个函数也都是原因（自变量）同时又
是结果（函数）。到目前，无论就自然科学还是哲学谁都没有找到，“世界的
起源”和“世界的终了”。
一说，黑洞是世界的终了，白洞是世界的起源。但据天体观察，远远大于黑白两
洞的宇宙存在指出，黑白洞也被包括在内，如星系中心往往是黑洞，但宇宙间
的星系太多了，这么多星系又从哪  里产生？到哪里去？
数学从来就是宇宙的“对称”。“自变量”并不自变，它也是因变的量；“因
变量”（函数）也并不就此终了，它也是自变量，引起在它之后的后果。
所以，“大循环图象”中的自变量是外界影响的结果，它的因变量又去影响外
界，两个端点都必然与外界联系。
正如，数学里常常引入“参量方程”。
ρ２＝ｘ２＋ｙ２
若ρ是常量，ｙ可以是ｘ的函数，ｘ是ｙ的自变量，只要给定一个ｘ数值必有
一个ｙ值对应存在。但是现在要引入“参量”：
ｘ＝ρ　ｃｏｓφ
ｙ＝ρ　ｓｉｎφ
这意思是说，ｘ与ｙ又是φ的函数，φ是ｘ与ｙ的共同自变量。于是“ｘ是ｙ
的自变量”被引入的φ所否定，ｘ又成了φ的函数，成为一种结果，不是原因
了。
但数学里只是以“引入参量”给出，甚至这个被引入的参量具体数学形式都不
必写出，而是“引入参量ｘ＝φ（ｔ），ｙ＝ψ（ｔ）”代替多种的参量形式
。常此下去，习以为常，人们都知道变量是存在“参量关系”的，因为“事实
如此”，其实这种承认和接受，等于人们不自觉的而是自发地承认了“自变量不是终极原因，函数也不是终极结果”。
“大循环图象”也如此，它只是表现有限个中间环节、函数的存在
的内部关系是守恒的，未涉及它的外部原因和对外影响，但不等于
说它是“极度封闭”的与外界无关。
当然，从哲学上说，“丢掉高阶无穷小”也不是守恒的，如丢掉一阶无穷小的
例子
ｙ＝ｘ２
ｙ＋Δｙ＝（ｘ＋Δｘ）２
Δｙ＝２ｘΔｘ＋Δｘ２
ΔｙΔｘ＝２ｘ＋Δｘ
ｌｉｍΔｘ→０
Δｙ
Δｘ＝２ｘ——（２ｘ）
但这里，在数学上“取Δｘ→０时ΔｙΔｘ的极限”，Δｘ→０，就可以丢掉第二项Δｘ。尽管Δｘ
是无穷小，趋近于零，它仍然还是个“存在”,并非是“无”。数学认为这种“存
在”就是“无”。
守恒概念应当否认（２ｘ）式的存在，但事实它存在，数学概念承认它。
同样道理，“大循环图象”既是守恒的又与外界有关联，有影响（自变量接受
外界影响、函数影响外界），受数学“法权”保护。
上述的数学过程产生如下排列“大循环图象”的原则：
（１）它必须是循环所属的。
（２）正函数守恒与反函数守恒是对称的。
（３）正函数的自变量是反函数的函数，反函数的自变量又是正函数的函数。
（４）正函数与反函数的自变量、函数在“对称所属循环”中，它们仅仅是两种不同的“端量”，已经无所谓自变量，因变量（函
数）之称。一端接受来自大循环内部对称方的影响，同时又施影响于大循环外
部，另一端也同样施影响于大循环的外部同时又接受来自大循环对称方的影
响，所以排列时要求同一个端量必须排列在两端上，如ｘ占端的图象中四个ｘ
排列在上下之端；ｙ占端的图象中四个ｙ排列在上下之端。可见，端量必须是
施影响于大循环之外；又受外影响的量占有，此为特征。
我们将一周分为８个象限，只因有４个变量ｙ、ｕ、ｖ、ｘ、别无它因，分为
几个象限都决定于变量的多寡。按解析几何习惯，平面圆被均分的部分称为象
限。
（５）“循环所属”与“对称”组成“对称所属循环”，这种循环要求每个象
限为同一个变量占有。
（６）组成大循环图象后，原有的两个量间的除法关系不变，共有８个除法关
系。或者说，每个象限为一种变量占有充填的内容，则两个象限的关系是以其
内容“（变量）的除法关系建立的。
（７）排列方向以逆时针方向为正向，顺时针方向为反向。
“大循环图象”在现有的逻辑阶段，仍然处在低级的抽象之中，只有进入自然
描绘的阶段，才能上升为高级的具体。
这项理论，是产生一系列“运动论的物理学结论”的原因和数学模型。