一个历史的误差











选自《运动论》第34页
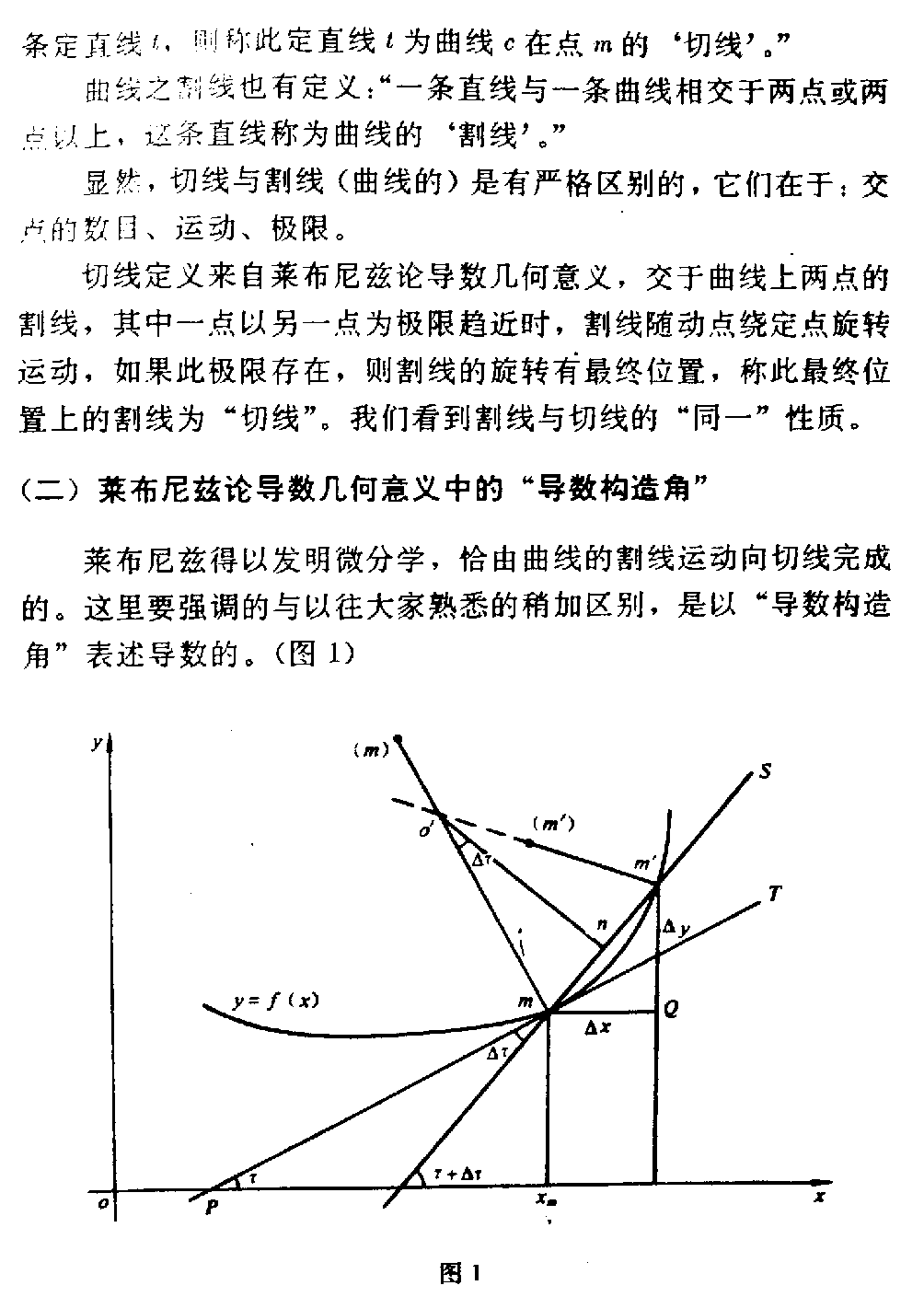
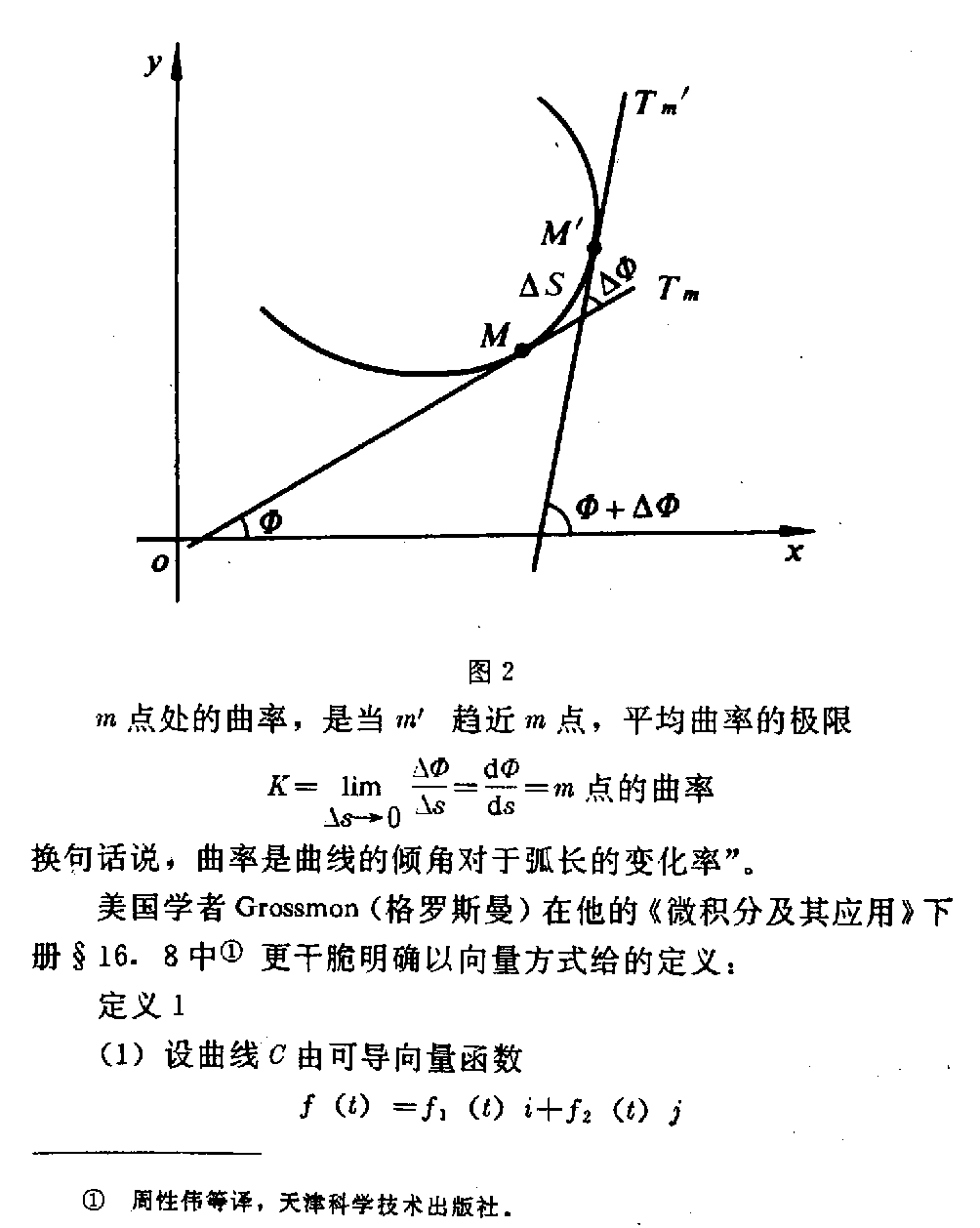
下载一个历史的误差 数学里,甲乙两不同基础概念树立的两个关系式中,当自变量 趋近无穷大或无穷小时,两关系同时趋近同一个极限,有共同的确定函数存在 ,但我们不能因此将两个基础概念也等同起来看待是很常见的事。 在此类问题中,为了取得甲概念的极限而确定的定量关系,却使用乙概念及其 关系来推演,以为“结论正确”,很可能造成概念混淆之误。例如,圆内接正 多边形边数趋近无穷大时的面积与圆外切正多边形的边数趋近无穷大的面积是 同一个函数,但它们的基础概念截然不同,如果说它们各自有新发展,时至今 日已经分道扬镳,千差万别了。 “一个历史的误差”正在此类逻辑交点上,它就是:曲线上两点之切线夹角对 于其对应弧长的变化率 dΦ/dSΦ 和交于曲线上两点之割线与过其中一点的切线之夹角对于其对应弧长的变化率 dτ/dSτ 的异同引起的。 因此,我愿意历史地把原理先陈述清楚,然后看“误”在哪里,最后再翻一翻 历史,可能或希望引起大家沉思。 (一)切线与割线的区别和“同一” 曲线之切线被定义为:“过曲线c上一点m及另一点m作割 线L,当点m沿曲线无限地趋近于点m时,如果直线L趋近于一条定直线t, 则称此定直线t为曲线c在点m的‘切线’。” 曲线之割线也有定义:“一条直线与一条曲线相交于两点或两点以上,这条直 线称为曲线的‘割线’。”显然,切线与割线(曲线的)是有严格区别的,它们在于:交 点的数目、运动 、极限。 切线定义来自莱布尼兹论导数几何意义,交于曲线上两点的割线,其中一点以 另一点为极限趋近时,割线随动点绕定点旋转运动,如果此极限存在,则割线 的旋转有最终位置,称此最终位置上的割线为“切线”。我们看到割线与切线 的“同一”性质。 (二)莱布尼兹论导数几何意义中的“导数构造角” 莱布尼兹得以发明微分学,恰由曲线的割线运动向切线完成的 。这里要强调的与以往大家熟悉的稍加区别,是以“导数构造角”表述导数的 。(图1) 图1 由莱布尼兹的几何关系,总有 ΔyΔx=tg(τ+Δτ) 当自变量的增量Δx→0时,使Δy→0,Δτ→0,达到极限 状态,记为 lim Δx→0ΔyΔx=limΔτ→0tg(τ+Δτ) 简作dydx=tgτ ——(tgτ)Δx→0 我们看到,割线与切线差别的定量完全体现在有无Δτ。如果割线有斜率,则 是 tg(τ+Δτ)如果切线有斜率,则是 limm′→mtg(τ+Δτ) =tgτ——(tgτ)m′→m 我们已经知道,之所以取这个极限表示割线与切线间的关系完全在于表现运动 ,同时对于函数y=f(x),正切值又是它的导数,可以描绘函数运动特性 的关系正是割线运动向切线的导数。但是,我们这里仅从最原始的几何概念出 发,不用“Δx→0”,而用“动点m’运动趋向于m点”表示,成为一切结 果的原因。 显见limm′→mΔτ =dτ 0 角dτ称为“构造函数之导数的微角”,简称“导数构造角”。它特指 割线S向切线T的动态特性,由于它的存在,导数概念才能确立。 使用m′沿曲线趋近m(m′→m)的最大好处是,它囊括有“Δx→0”、 “Δy→0”、“Δτ→0”三量的动向,反之则不能。所以原始几何的逻辑 符号具有取代函数坐标的性质,称这种导数表示法为“不确定函数坐标的函数之导 数等于正切值”表示法。 (三)割线与切线夹角Δτ和“半径 转角”ΔΦ的差别 1.曲线为圆时,半径乘以转角等于弧长 R·ΔΦ=S——(S) 转角ΔΦ还等于曲线上对应ΔΦ角两端点处m与m之切线 交角(<90°) 2.一般函数,弧对于转角的导数等于半径 dsdΦ=Rm——(Rm) 也是(S)式的微分式。 定义Rm为m点 的曲率半径,其倒数1/Rm定义为m点处曲线的曲率 。 必须加以特殊明确的是dΦ不是导数构造角dτ 。dΦ是T′m→Tm(即S→T)相交成的微补角, 无论ΔΦ还是dΦ都是m与m点处两切线的交角。这是个很容易 分辨的事情,往往不为人们注意,致使出现“误差”。 证明指出 dΦ=2dτ 也有dSΦ=2d Sτ dSΦ——d Φ对应的微弧长, dSτ——dτ对应的微弧长, 对于曲线上某点的曲率与曲率半径要从切线方向的改变考虑,如苏联科学院已 故院士H.H.Лузин(鲁金)在他的著名《微分学》第十 四章中写到“m是曲线上接近于m的第二个点。当切线的切点绘出 mm弧(=ΔS)时,切线转动了ΔΦ角,这就是说,ΔΦ 是切线方向的变化,作下面定义:(图2) ΔΦΔS=曲线弧mm的平均曲率 图2 m点处的曲率,是当m趋近m点,平均曲率的极限 K=limΔs→0ΔΦ Δs =dΦds=m点的曲率 换句话说,曲率是曲线的倾角对于弧长的变化率”。 美国学者Grossmon(格罗斯曼)在他的《微积分及其 应用》下册§16.8中周性伟等译,天津科学技术出版社。更干脆明确以向量方式给的定义: 定义1 (1)设曲线C由可导向量函数 f(t)=f1(t)i+f2(t)j 给出,用φ(t)表示f(t)的方向。所谓C的曲率,就是指方向关于弧 长的变化率的绝对值,即 K(t)= dφdS 其中K(t)称为曲线的曲率 (2)所谓曲率半径ρ(t)定义为 ρ(t)=1K(t) 定理一 设T(t)表示f的单位切向量,则 K(t)= dTd S 由于φ是f的方向,因而也是T的方向,所以 T=(cosφ)i+(sinφ)j dTdφ=-(sinφ)i+(cosφ)j dTdφ =cos2φ +sin2φ=1 则 dTdS= dTdφ dφds=1· dφd S=K(t) 这个证明指出“C的曲率就是指方向关于弧长的变化率”,因之“φ是f的 方向”、“T(t)表示f的单位切向量”是正确的。 两位学者所论曲率问题均使用切线及切线方向关于弧长的变化率概念,基本概 念一致,dΦ、dφ都是曲率半径的微转角,等于曲线上微分ds两端点m、m之切线的交角(<90°), 因之不是导数构造角dτ 仍如图一,有关系 ΔΦ=∠mom=Δτ+∠mon 当m→m时,(m)→(m),o→(m),弧mm成为“密切圆” 的一部分弧(根据定理,密切圆恒等于曲率圆。H.H.Лузин(鲁金),微分学,§147。) 即 limm′→mΔΦ= limm→mΔτ +limm→m∠mon 其中limm→mΔτ =limm→m∠mon =dτ limm→mΔ Φ=dΦ 故dΦ= dτ+ dτ =2dτ 此即密切圆的微圆心角。各角的对应弧也有 dSΦ=2·dSτ 这就是曲线之割线与切线夹角Δτ与曲率半径 微转角ΔΦ在极限状态的区别。 (四)历史的误差 这是将“导数构造角”应用于求证曲率引起的。 1.基本概念与原理对于数学应用一致的实例。 若使用dτ角求曲率1/Rm,必须将dΦ及ds变换成 dτ后才能使用,不能直接以此代dΦ使用。 K=1Rm=dΦdSΦ 因dΦ=2dτ dSΦ=2dSτ K=1Rm= 2d τ2dSτ =dτd Sτ 又因y=tgτdyd x=yτ=Arctgy dτ=y″1+y2 dx dSτ=1+y2·dx 故1Rm=y″(1 +y2)3/2 Rm=(1+y2)3/2 y″ 结果是正确的。 造成“历史的误差”就在于,曲率概念乃d Φ/dSΦ,不是dτ/d Sτ。尽管两个比的数值相等,其本质含意与概念是不能等 同的。 2.仍以前两位学者(鲁氏和格氏)为代表,误以dτ代替dΦ求曲率的证法 格罗斯曼的证法格罗斯曼微积分及其应用,天津科学技术出版社,下册 ,第183页。 “假如一个曲线是由笛卡尔方程y=f(x)给出的,则它的曲 率公式较为简单。我们用K(x)表示这个曲线的曲率,我们有 dφdx=dφdS·dSdx 或dφdS=dφ/dxdS/d x ds dx=1+(dφ)dx)2 由于tgφ=dy/dx(此处原书有误,少写tg) 我们有φ=tg1dydx dφdx=11+(dy/dx )2·d2y dx2 所以K(x)=| dφds|= |d2y/dx2|[1+(dy/d x)2]3/2” 尽管格罗斯曼己经指明dφ为切向量夹角的微分,在这 里,显然他把“导数构造角”dτ当成了切向量夹角dΦ使用。当然 这是个错误。 鲁金的证法H.H.Лузин(鲁金),微分学,§133。 “定理:设曲线的直角方程已知,则 K=y″(1+y2)3/2 其中y及y″是曲线的纵坐标y对于横坐标x的一阶及二阶导数。 因为τ=Arctgy′ 式中y=dydx 微分后得 dτdx=y″ 1+y2——(2) 另一方面 dSdx=(1+y2) 1/2——(3) 以(3)除(2)即得式(1)。”(注意他的dτ) 鲁金也犯了个与格罗斯曼相同的毛病,在他画的图与定义中指明了“曲率是曲 线的倾角对于弧长的变化率”,但在证明曲率公式时却使用曲线上两邻近点之 割线与一点的切线夹角的微分dτ,即将导数构造角当成两点切线夹角的 微角使用。 笔者查阅不少高校的高等数学教材,都存在同一问题,促使笔者联想到问题的 出处很可能由于建立导数与曲率概念时的异同引起。 笔者注意到: 1.莱布尼兹取得导数之几何意义建立的关系。 dydx=tgτ 恰恰与“当圆内正接多边形的边数n趋近无穷大n→∞时,正多边形的面积等 于圆面积”是一致的,此时正接多边形的边已完全与圆曲线贴切。 在莱布尼兹的概念中,“当m→m″正如正接多边形的一个边长趋近无穷小 过程,于是每个单边成为曲线上的微弧。但莱布尼兹是从正接多边形的一个单 边考虑取得与坐标的关系的。 2.惠更斯(Christian Huygens)最早证明“曲线上的点 沿固定法线到这极限位置的距离”。 [1+(dy/dx)2]3/2 d2y/dx2 这个长度是曲线在m点的曲率半径惠更斯,1673年,钟表的振 动,《古今数学思想》ⅡP301。,因此 Rm=dsφdφ= [1+(dy/dx)2]3/2d2y /dx2 这个算式是惠更斯研究渐伸线与渐屈线关系时取得的。 大家知道,曲率半径永远垂直渐伸线,切于渐屈线,因此曲率半径对于相对称 谓的渐伸线总是法线,对于其渐屈线总是切线。当渐伸线上有邻近两点,其中 一点m趋近固定点m时,在渐伸线上m与m点的两条切线相 交成的交角ΔΦ也趋近于零,使两点间的弧长ΔS也趋近于零,在极 限状态时,建立 Rm=dsφdφ 即所谓“曲线上的点沿固定法线到这极限位置的距离”m点的曲率半径。 这种运动状态又恰恰与“圆的外切正多边形的边数n趋近无穷大n→∞时,正 多边形的面积等于圆的面积”是一致的。但此时m→m恰如正切多边形的一 个边长趋近无穷小过程,只是考虑正切多边形的一个单边对应的弧长对于相邻两 边交角的变化率取得Rm的。 莱布尼兹是以曲线凹内正接多边形的一个单边趋于极 限的方法取得y=tgτ的;惠更斯则是以曲线凸上正 切多边形的一个单边趋于极限的类似方法取得Rm=dsφ /dφ的,可见两种方法依据的基础概念不同,但同时有 dΦdSΦ= 2dτ2dSτ =dτdSτ 两种导数相等(转角对于弧长的变化率)。 上两位学者的证法结果正确,但使用的原理容易使人混淆两种概念,严格说, 证明曲率应当用 K=dΦdSφ 不能用 K=dτdSτ (五)历史渊源与鉴证 应当看一看发现与发明曲率的人是怎样给曲率定义的,后来 是否有什么变化,与今日定义是否一致,可以为历史的鉴证。 英国学者M.Kline(克莱因)在他的《古今数学思想》Ⅱ.5.平面曲 线一节中(p302)引述了一段有关牛顿的论述: “牛顿在他的《解析几何》中(出版于1736年)也引进了曲 率中心,作为p点的法线及其邻点法线的交点的极限点。然后牛顿说,圆心在 曲率中心,半径等于曲率半径的圆是在p点与曲线最密接的圆;就是说,在曲 线和最密接圆之间,不会有别的圆在P点和曲线相切。这个最密接的圆叫做密 切圆,莱布尼兹在1686年的一篇文章中已经用了‘密切’这个术语。密切 圆的曲率是半径的倒数,而且是曲线在p点的曲率。牛顿也给出了曲率的公式 ,并计算了一些曲线,包括摆线在内的曲率。他注意到曲线在拐点处的曲率为 零。这些结果都是重复惠更斯的结果,但可能是牛顿想表明他能用解析方法来 建立这些结果。” 惠更斯早在1673年出版的《钟表的振动》已经求得曲率半 径,牛顿的《自然哲学的数学原理》1687年才出版,比惠更斯《钟表的振 动》晚了14年,牛顿的《流数法和无穷级数》一书直到1736年才出版古今数学思想,Ⅱ,P71。,其中他给出了曲率半径的正 确公式 r=(1+2)3/2 它的取作1。 莱布尼兹的工作更晚些。“但 他说直到1672年他还基本上不懂数学”“莱布尼兹从1684年起发表微积 分论文”,他的第一部著作《微分学的历史和起源》是1714年出版的见古今数学思想,Ⅱ,P82~83。。 可见惠更斯取得曲线某点曲率半径公式最早,牛顿则以解析法取得曲率半径最 早。 约1675年莱布尼兹在巴罗的“特征三角形”基础上建立了他的理论见古今数学思想,Ⅱ,P88。。 从中我们知道曲率、曲率半径的概念与公式早于莱布尼兹导数几何意义十几年 。使用莱布尼兹导数几何关系证明曲率公式是后人的事了。 但是,在微分几何的发展中,后人都延续了牛顿的曲线之曲率概念。在空间曲 线理论中,欧拉使用 dS′dS 表示曲率,dS′是曲线上相距dS(微弧)的两点的两个相邻切线 间的弧或角见古今数学思想,Ⅱ,P305。。柯西以他 自己的方法证明了 K=1ρ=dω dS 其中ω是相邻切线间的夹角见古今数学思想,Ⅱ,P308。 可见历史上一直认为曲率乃“相邻切线夹角”形成的,至今定义未加改变。 如果说是“历史的误差”,还查不到,繁衍至今,在哪儿形成的?
